
Question Number 69569 by Ajao yinka last updated on 25/Sep/19
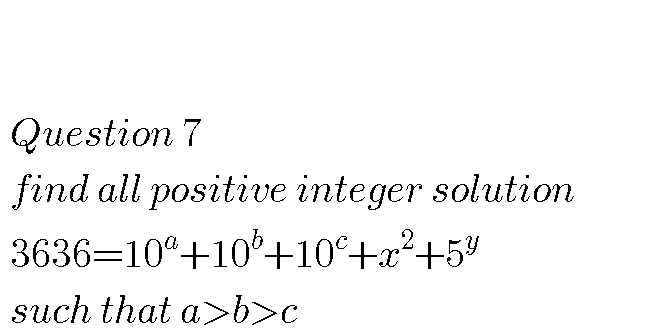
Answered by naka3546 last updated on 25/Sep/19
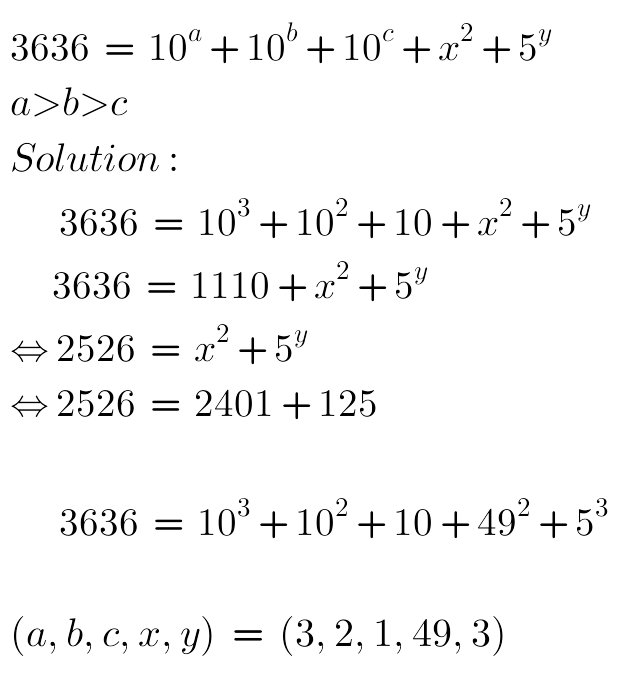
Commented by Rasheed.Sindhi last updated on 26/Sep/19
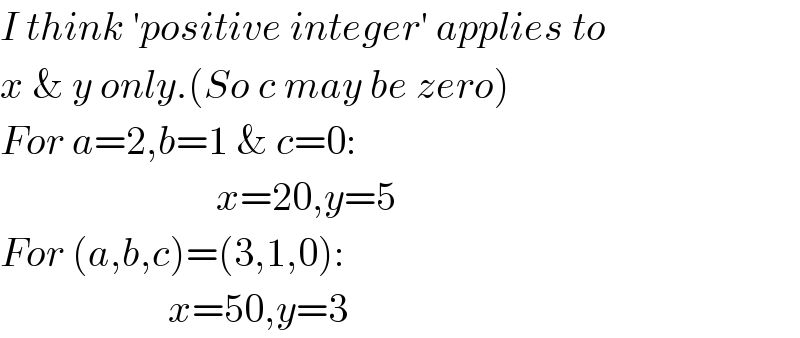
$${I}\:{think}\:'{positive}\:{integer}'\:{applies}\:{to} \\ $$$${x}\:\&\:{y}\:{only}.\left({So}\:{c}\:{may}\:{be}\:{zero}\right) \\ $$$${For}\:{a}=\mathrm{2},{b}=\mathrm{1}\:\&\:{c}=\mathrm{0}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{20},{y}=\mathrm{5} \\ $$$${For}\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{1},\mathrm{0}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{50},{y}=\mathrm{3} \\ $$
Commented by Ajao yinka last updated on 26/Sep/19

$${cool} \\ $$
Answered by Rasheed.Sindhi last updated on 27/Sep/19

$$\:\:\:\mathrm{10}^{{a}} \leqslant\mathrm{3636}\Rightarrow{a}<\mathrm{4} \\ $$$${a}>{b}>{c}: \\ $$$${possibilities}\:{for}\:\left({a},{b},{c}\right) \\ $$$$\left(\mathrm{3},\mathrm{2},\mathrm{1}\right),\left(\mathrm{3},\mathrm{2},\mathrm{0}\right),\left(\mathrm{3},\mathrm{1},\mathrm{0}\right),\left(\mathrm{2},\mathrm{1},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\underset{−} {\:\:\:\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{1}\right)\:\:\:\:\:} \\ $$$$\:\:\:\:\mathrm{10}^{\mathrm{3}} +\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{1}} +{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636}−\mathrm{1110}=\mathrm{2526} \\ $$$$\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{2526}−\mathrm{5}^{{y}} } \\ $$$${Testing}\:{for}\:{y}=\mathrm{1},\mathrm{2},\mathrm{3},... \\ $$$${x}\in\mathbb{Z}^{+} \:{only}\:{for}\:{y}=\mathrm{3} \\ $$$$\therefore\:{for}\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{1}\right):\:{y}=\mathrm{3},{x}=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\underset{−} {\:\:\:\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{0}\right)\:\:\:\:\:} \\ $$$$\:\:\mathrm{10}^{\mathrm{3}} +\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{0}} +{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636}−\mathrm{1101}=\mathrm{2535} \\ $$$$\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{2535}−\mathrm{5}^{{y}} } \\ $$$${x}\:{is}\:{positive}\:{integer}\:{for}\:{no}\:{value}\:{of}\:{y}. \\ $$$$\therefore\:{No}\:{solution}\:{in}\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{0}\right). \\ $$$$\:\:\:\:\:\:\:\:\underset{−} {\:\:\:\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{1},\mathrm{0}\right)\:\:\:\:\:} \\ $$$$\:\:\:\mathrm{10}^{\mathrm{3}} +\mathrm{10}^{\mathrm{1}} +\mathrm{10}^{\mathrm{0}} +{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636} \\ $$$$\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{2625}−\mathrm{5}^{{y}} } \\ $$$${y}=\mathrm{3}\Rightarrow{x}=\mathrm{50}\:\left({only}\:{positive}\:{integers}\right) \\ $$$$\therefore\:{for}\:\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{1},\mathrm{0}\right):{y}=\mathrm{3},{x}=\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\:\underset{−} {\:\:\:\:\:\:\left({a},{b},{c}\right)=\left(\mathrm{2},\mathrm{1},\mathrm{0}\right)\:\:\:\:\:} \\ $$$$\:\:\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{1}} +\mathrm{10}^{\mathrm{1}} +{x}^{\mathrm{2}} +\mathrm{5}^{{y}} =\mathrm{3636} \\ $$$$\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{3525}−\mathrm{5}^{{y}} } \\ $$$$\:\:{y}=\mathrm{5}\Rightarrow{x}=\mathrm{20}\:\left({only}\:{positive}\:{integers}\right)\: \\ $$$$\therefore{for}\:\left({a},{b},{c}\right)=\left(\mathrm{2},\mathrm{1},\mathrm{0}\right):\:{y}=\mathrm{5},{x}=\mathrm{20} \\ $$$$ \\ $$$$\begin{cases}{\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{1}\right):\left({x},{y}\right)=\left(\mathrm{49},\mathrm{3}\right)}\\{\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{2},\mathrm{0}\right):\left({x},{y}\right)=\phi}\\{\left({a},{b},{c}\right)=\left(\mathrm{3},\mathrm{1},\mathrm{0}\right):\left({x},{y}\right)=\left(\mathrm{50},\mathrm{3}\right)}\\{\left({a},{b},{c}\right)=\left(\mathrm{2},\mathrm{1},\mathrm{0}\right):\left({x},{y}\right)=\left(\mathrm{20},\mathrm{5}\right)}\end{cases} \\ $$$$ \\ $$
Commented by Ajao yinka last updated on 27/Sep/19
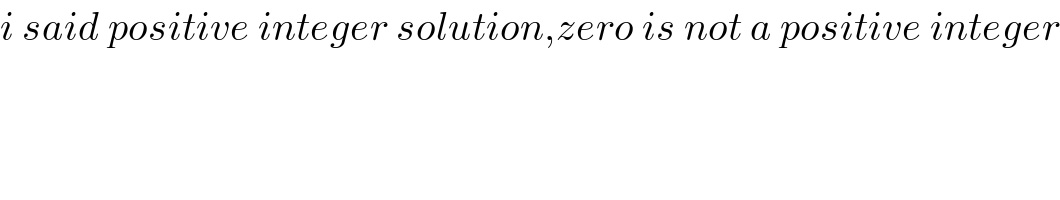
$${i}\:{said}\:{positive}\:{integer}\:{solution},{zero}\:{is}\:{not}\:{a}\:{positive}\:{integer} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Sep/19

$${a},{b}\:\&\:{c}\:{are}\:\boldsymbol{{arbitrary}}\:\boldsymbol{{constant}}{s}\:{and}\:{x}\:\&\:{y}\:{are} \\ $$$${variables}.\:{The}\:{condition}\:``{positive}\:{integersip}'' \\ $$$${are}\:{aplicable}\:{to}\:{variables}\:{here}. \\ $$
