
Question Number 69568 by Ajao yinka last updated on 25/Sep/19
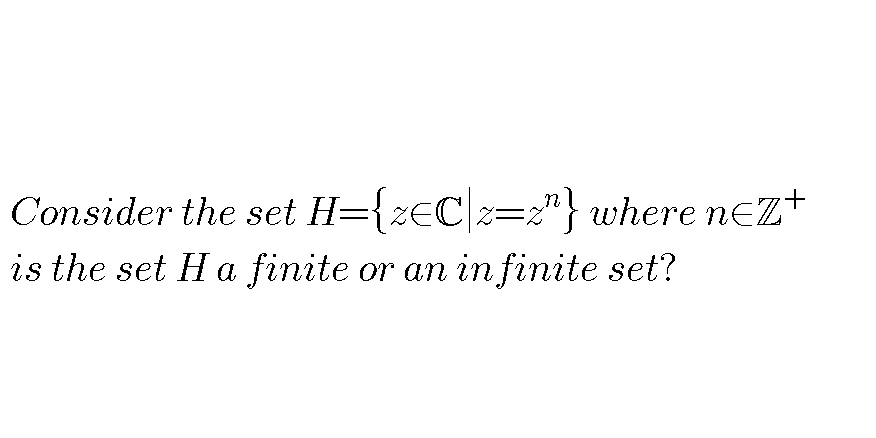
Commented by mathmax by abdo last updated on 25/Sep/19
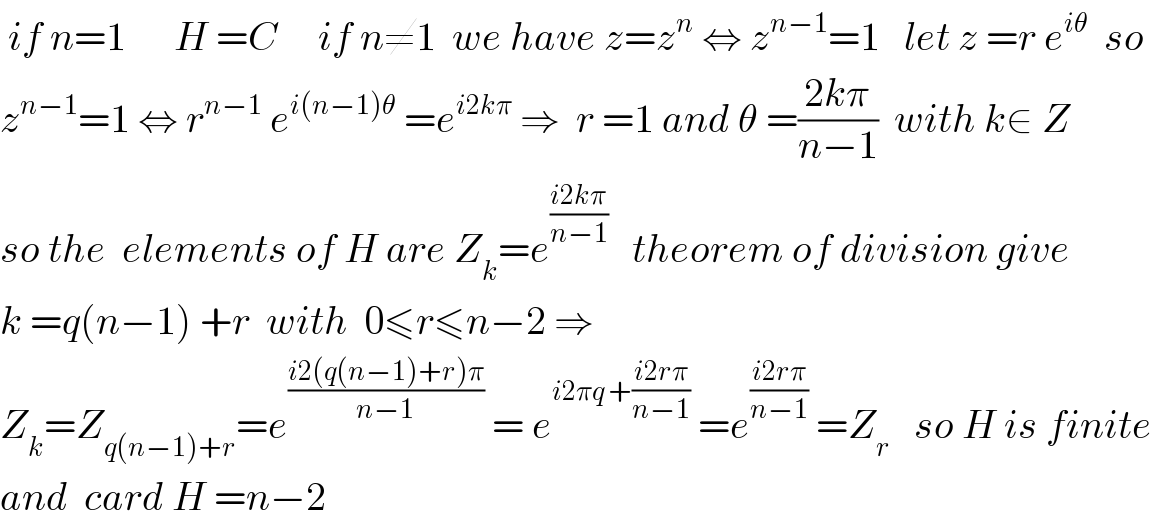
$$\:{if}\:{n}=\mathrm{1}\:\:\:\:\:\:{H}\:={C}\:\:\:\:\:{if}\:{n}\neq\mathrm{1}\:\:{we}\:{have}\:{z}={z}^{{n}} \:\Leftrightarrow\:{z}^{{n}−\mathrm{1}} =\mathrm{1}\:\:\:{let}\:{z}\:={r}\:{e}^{{i}\theta} \:\:{so} \\ $$$${z}^{{n}−\mathrm{1}} =\mathrm{1}\:\Leftrightarrow\:{r}^{{n}−\mathrm{1}} \:{e}^{{i}\left({n}−\mathrm{1}\right)\theta} \:={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow\:\:{r}\:=\mathrm{1}\:{and}\:\theta\:=\frac{\mathrm{2}{k}\pi}{{n}−\mathrm{1}}\:\:{with}\:{k}\in\:{Z} \\ $$$${so}\:{the}\:\:{elements}\:{of}\:{H}\:{are}\:{Z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}−\mathrm{1}}} \:\:\:{theorem}\:{of}\:{division}\:{give} \\ $$$${k}\:={q}\left({n}−\mathrm{1}\right)\:+{r}\:\:{with}\:\:\mathrm{0}\leqslant{r}\leqslant{n}−\mathrm{2}\:\Rightarrow \\ $$$${Z}_{{k}} ={Z}_{{q}\left({n}−\mathrm{1}\right)+{r}} ={e}^{\frac{{i}\mathrm{2}\left({q}\left({n}−\mathrm{1}\right)+{r}\right)\pi}{{n}−\mathrm{1}}} \:=\:{e}^{{i}\mathrm{2}\pi{q}\:+\frac{{i}\mathrm{2}{r}\pi}{{n}−\mathrm{1}}} \:={e}^{\frac{{i}\mathrm{2}{r}\pi}{{n}−\mathrm{1}}} \:={Z}_{{r}} \:\:\:{so}\:{H}\:{is}\:{finite} \\ $$$${and}\:\:{card}\:{H}\:={n}−\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 26/Sep/19
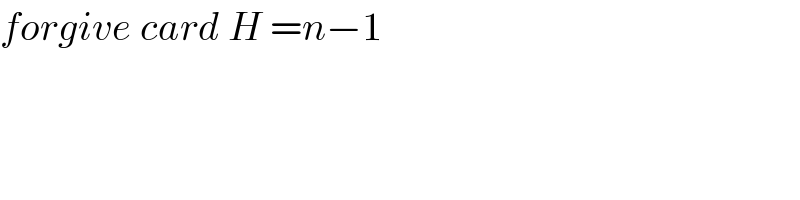
$${forgive}\:{card}\:{H}\:={n}−\mathrm{1} \\ $$
Commented by Ajao yinka last updated on 26/Sep/19
$${so}\:{whats}\:{your}\:{conclusion} \\ $$
Answered by mind is power last updated on 25/Sep/19
![H={z∈C∣z^n −z=0} H is set of roots/of P(X)=X^n −X∈C_n [X] C is a field So integer domain ⇒card(h)≤Deg(P)=n So finite](Q69632.png)
$${H}=\left\{{z}\in\mathbb{C}\mid{z}^{{n}} −{z}=\mathrm{0}\right\} \\ $$$${H}\:{is}\:{set}\:{of}\:{roots}/{of}\:{P}\left({X}\right)={X}^{{n}} −{X}\in\mathbb{C}_{{n}} \left[{X}\right] \\ $$$$\mathbb{C}\:{is}\:{a}\:{field}\:{So}\:{integer}\:{domain}\:\Rightarrow{card}\left({h}\right)\leqslant{Deg}\left({P}\right)={n} \\ $$$${So}\:{finite}\: \\ $$$$ \\ $$
