
Question Number 69566 by Ajao yinka last updated on 25/Sep/19
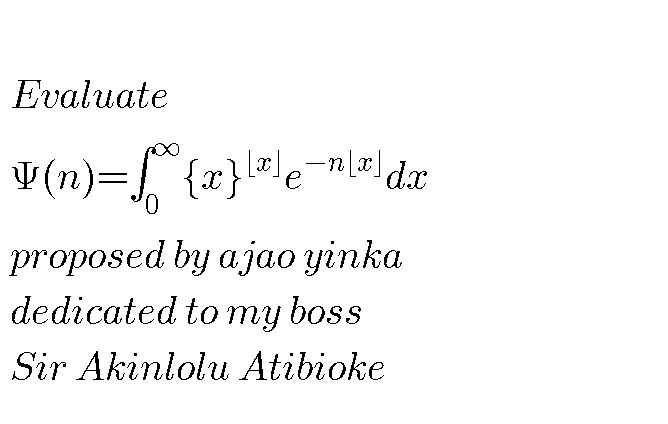
Answered by mind is power last updated on 25/Sep/19
![=lim_(x→+∞) Σ_(k=0) ^x ∫_k ^(k+1) (x−k)^k e^(−nk) dx =lim_(x→+∞) Σ_(k=0) ^x e^(−nk) ∫_k ^(k+1) (x−k)^k dx =lim_(x→+∞) Σ_(k=0) ^x e^(−nk) [(((x−k)^(k+1) )/(k+1))]_k ^(k+1) =lim_(x→+∞) Σ_(k=0) ^x e^(−nk) .(1/(k+1)) A=lim_(x→+∞) Σ_(k=0) ^x e^(−(k+1)n) .(e^n /(k+1)) we have −ln (1−x)=Σ_(k=0) ^(+∞) (x^(k+1) /(k+1)) A=e^n Σ_(k=0) ^(+∞) (((e^(−n) )^(k+1) )/(k+1))=e^n ×−ln(1−e^(−n) )=e^n ln((1/(1−e^(−n) )))=e^n ln ((e^n /(e^n −1)))=e^n (n−ln(e^n −1))](Q69633.png)
$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sum_{{k}=\mathrm{0}} ^{{x}} \int_{{k}} ^{{k}+\mathrm{1}} \left({x}−{k}\right)^{{k}} {e}^{−{nk}} {dx} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sum_{{k}=\mathrm{0}} ^{{x}} {e}^{−{nk}} \int_{{k}} ^{{k}+\mathrm{1}} \left({x}−{k}\right)^{{k}} {dx} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sum_{{k}=\mathrm{0}} ^{{x}} {e}^{−{nk}} \left[\frac{\left({x}−{k}\right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\right]_{{k}} ^{{k}+\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sum_{{k}=\mathrm{0}} ^{{x}} {e}^{−{nk}} .\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$${A}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\sum_{{k}=\mathrm{0}} ^{{x}} {e}^{−\left({k}+\mathrm{1}\right){n}} .\frac{{e}^{{n}} }{{k}+\mathrm{1}} \\ $$$$ \\ $$$${we}\:{have}\:−\mathrm{ln}\:\left(\mathrm{1}−{x}\right)=\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}} \\ $$$${A}={e}^{{n}} \underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\left({e}^{−{n}} \right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}={e}^{{n}} ×−{ln}\left(\mathrm{1}−{e}^{−{n}} \right)={e}^{{n}} {ln}\left(\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{n}} }\right)={e}^{{n}} \mathrm{ln}\:\left(\frac{{e}^{{n}} }{{e}^{{n}} −\mathrm{1}}\right)={e}^{{n}} \left({n}−{ln}\left({e}^{{n}} −\mathrm{1}\right)\right) \\ $$$$ \\ $$
Commented by Ajao yinka last updated on 26/Sep/19

$${perfect}\:{solution} \\ $$
