
Question Number 6944 by Tawakalitu. last updated on 03/Aug/16
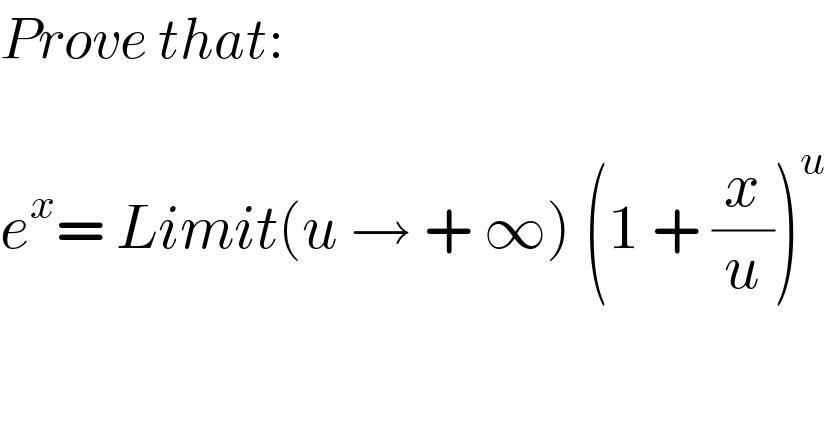
$${Prove}\:{that}: \\ $$$$ \\ $$$${e}^{{x}} =\:{Limit}\left({u}\:\rightarrow\:+\:\infty\right)\:\left(\mathrm{1}\:+\:\frac{{x}}{{u}}\right)^{{u}} \: \\ $$
Answered by sou1618 last updated on 03/Aug/16
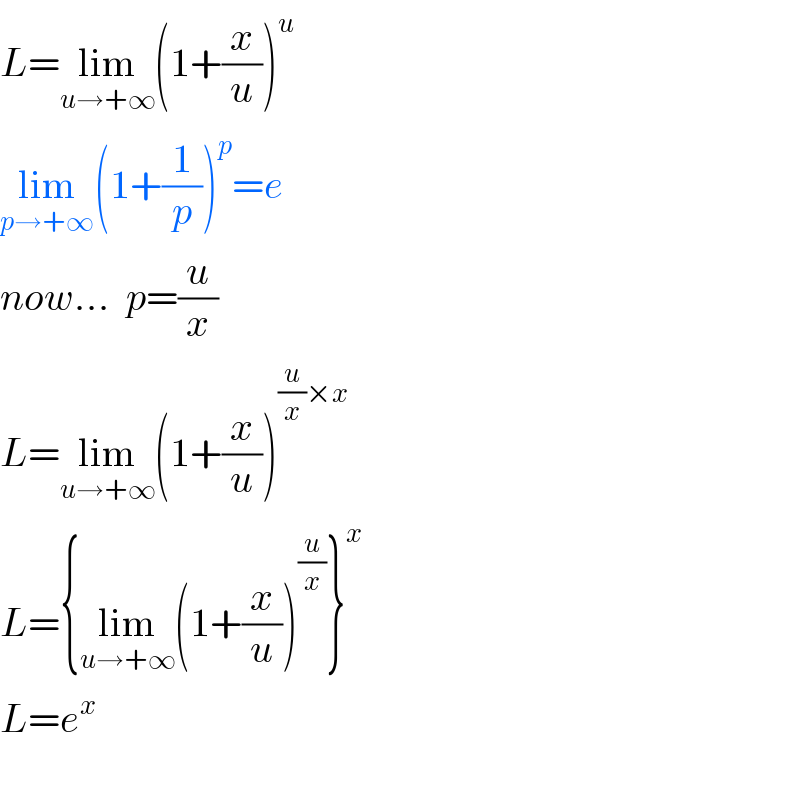
$${L}=\underset{{u}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}}{{u}}\right)^{{u}} \\ $$$$\underset{{p}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{p}}\right)^{{p}} ={e} \\ $$$${now}...\:\:{p}=\frac{{u}}{{x}} \\ $$$${L}=\underset{{u}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}}{{u}}\right)^{\frac{{u}}{{x}}×{x}} \\ $$$${L}=\left\{\underset{{u}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}}{{u}}\right)^{\frac{{u}}{{x}}} \right\}^{{x}} \\ $$$${L}={e}^{{x}} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 03/Aug/16
$${Thank}\:{you}\:{very}\:{much} \\ $$
Answered by FilupSmith last updated on 03/Aug/16
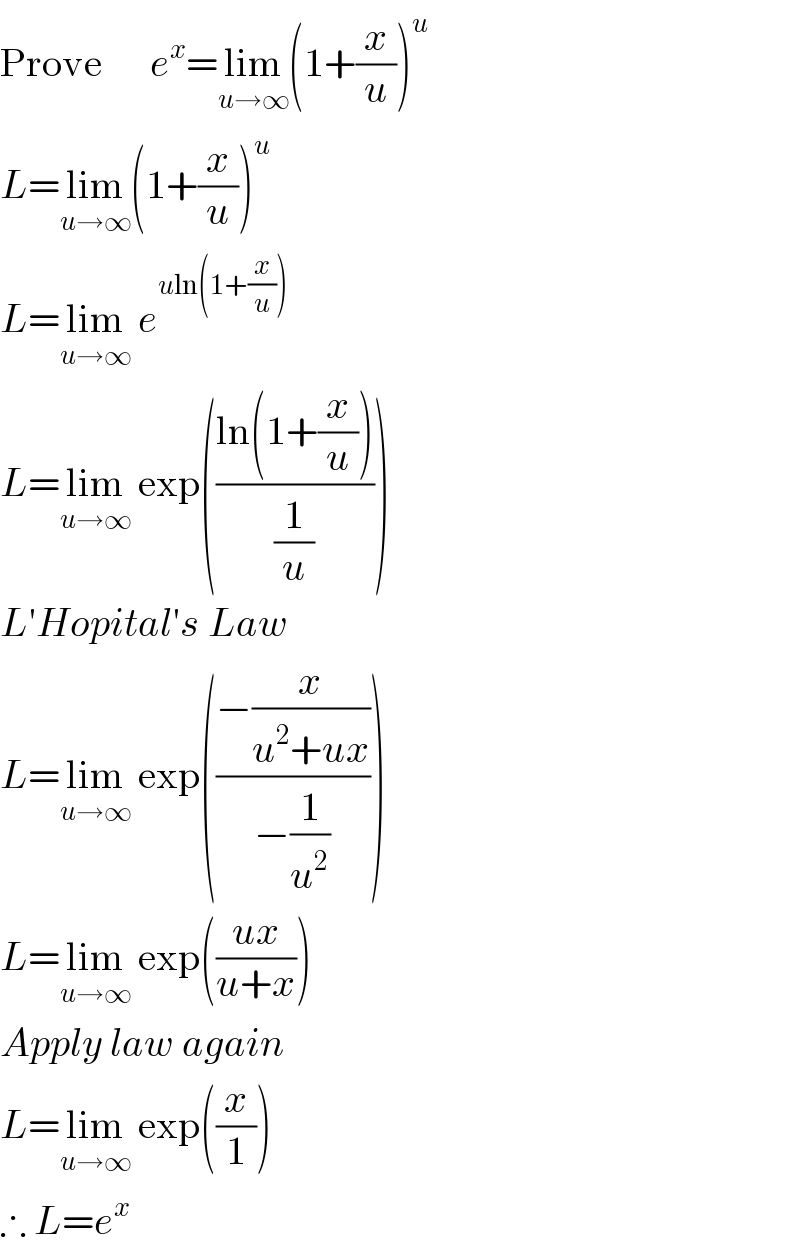
$$\mathrm{Prove}\:\:\:\:\:\:{e}^{{x}} =\underset{{u}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}}{{u}}\right)^{{u}} \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{x}}{{u}}\right)^{{u}} \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:{e}^{{u}\mathrm{ln}\left(\mathrm{1}+\frac{{x}}{{u}}\right)} \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{exp}\left(\frac{\mathrm{ln}\left(\mathrm{1}+\frac{{x}}{{u}}\right)}{\frac{\mathrm{1}}{{u}}}\right) \\ $$$${L}'{Hopital}'{s}\:{Law} \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{exp}\left(\frac{−\frac{{x}}{{u}^{\mathrm{2}} +{ux}}}{−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}\right) \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{exp}\left(\frac{{ux}}{{u}+{x}}\right) \\ $$$${Apply}\:{law}\:{again} \\ $$$${L}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{exp}\left(\frac{{x}}{\mathrm{1}}\right) \\ $$$$\therefore\:{L}={e}^{{x}} \\ $$
Commented by Tawakalitu. last updated on 03/Aug/16

$${Thanks}\:{so}\:{much} \\ $$
