
Question Number 69398 by Tony Lin last updated on 23/Sep/19

Commented by Tony Lin last updated on 23/Sep/19

$${Solve}\:\mathrm{53}.\&\mathrm{55}. \\ $$
Answered by mr W last updated on 24/Sep/19
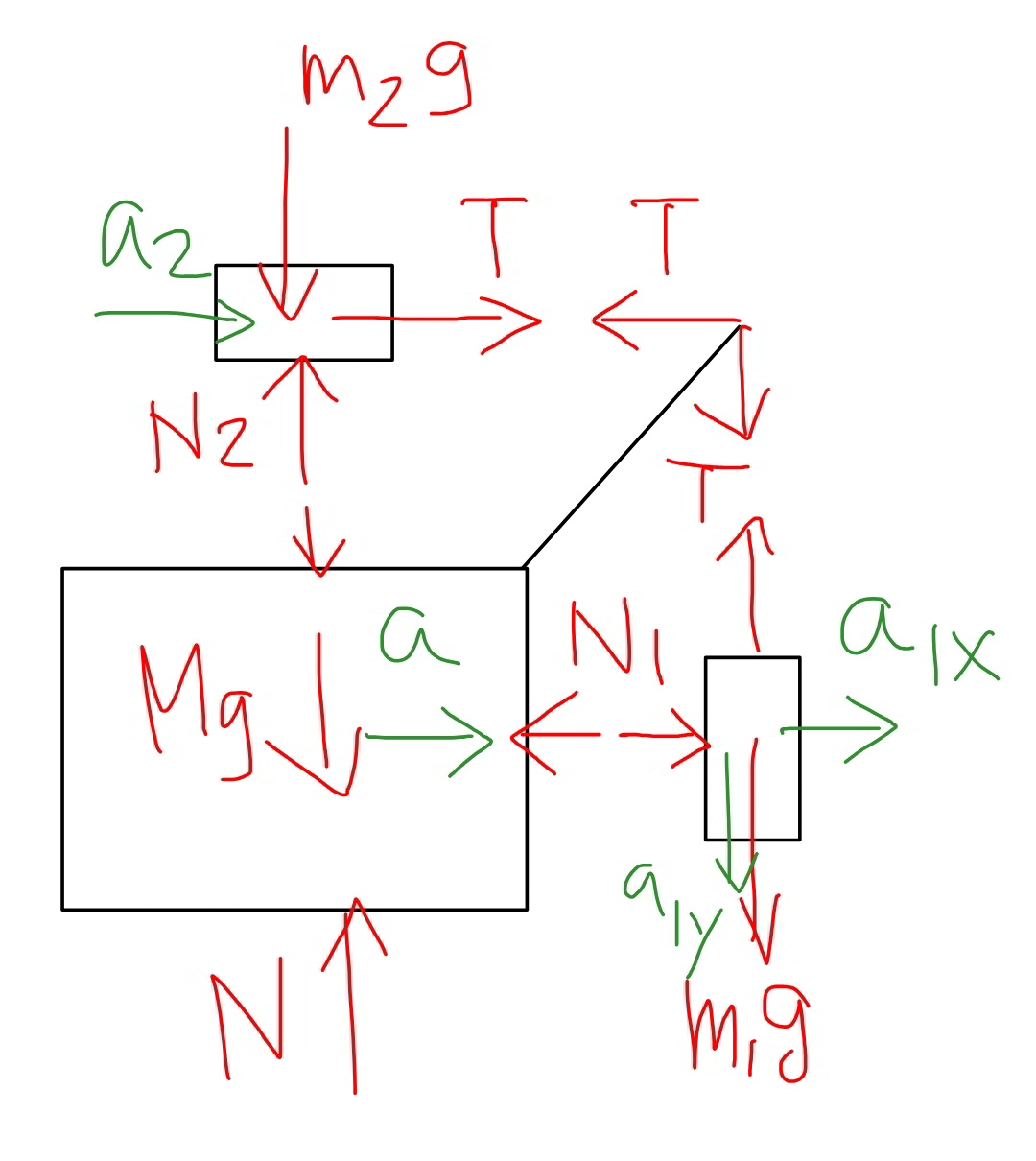
Answered by mr W last updated on 23/Sep/19
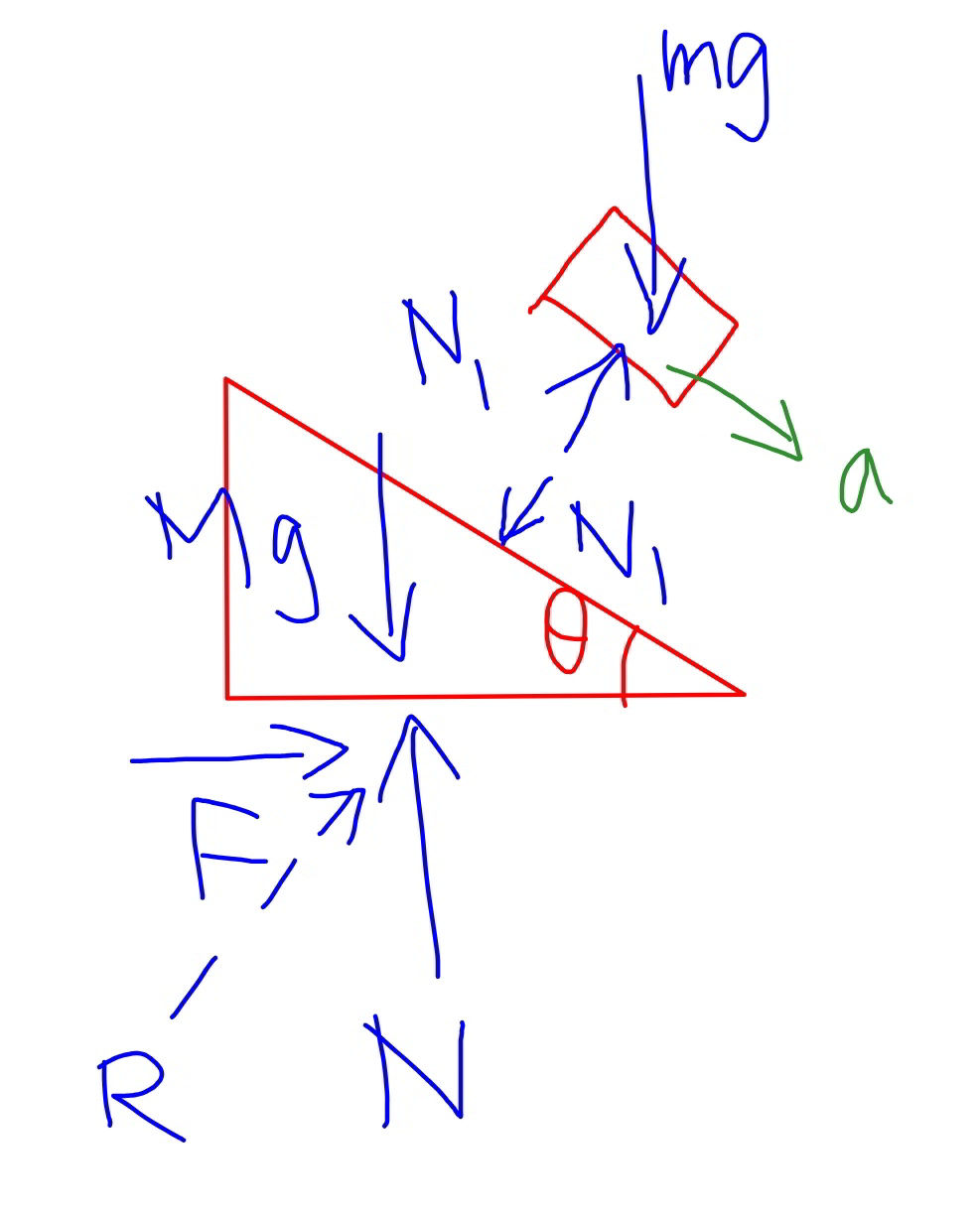
Commented by mr W last updated on 24/Sep/19
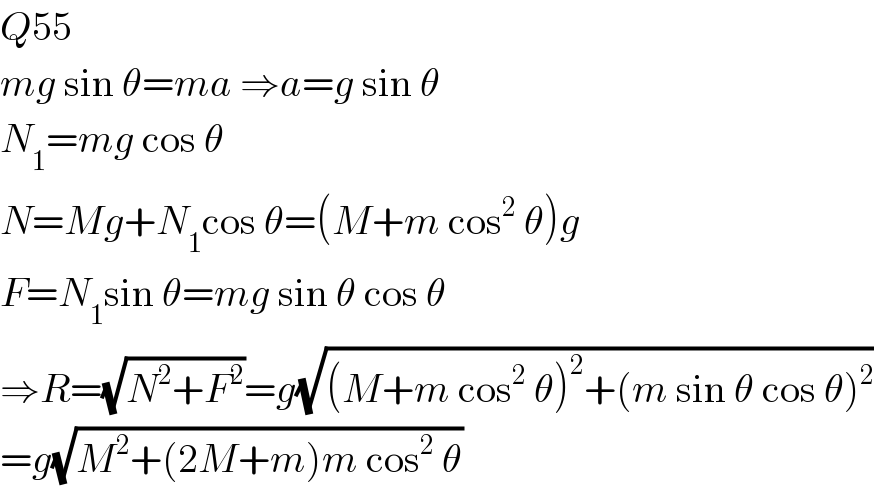
$${Q}\mathrm{55} \\ $$$${mg}\:\mathrm{sin}\:\theta={ma}\:\Rightarrow{a}={g}\:\mathrm{sin}\:\theta \\ $$$${N}_{\mathrm{1}} ={mg}\:\mathrm{cos}\:\theta \\ $$$${N}={Mg}+{N}_{\mathrm{1}} \mathrm{cos}\:\theta=\left({M}+{m}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right){g} \\ $$$${F}={N}_{\mathrm{1}} \mathrm{sin}\:\theta={mg}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{R}=\sqrt{{N}^{\mathrm{2}} +{F}^{\mathrm{2}} }={g}\sqrt{\left({M}+{m}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} +\left({m}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} } \\ $$$$={g}\sqrt{{M}^{\mathrm{2}} +\left(\mathrm{2}{M}+{m}\right){m}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$
