
Question Number 6922 by Tawakalitu. last updated on 02/Aug/16

$${x}^{{y}} \:=\:{y}^{{x}} \\ $$$$ \\ $$$${make}\:{x}\:{the}\:{subject}\:{of}\:{the}\:{formular} \\ $$
Commented by Yozzii last updated on 03/Aug/16
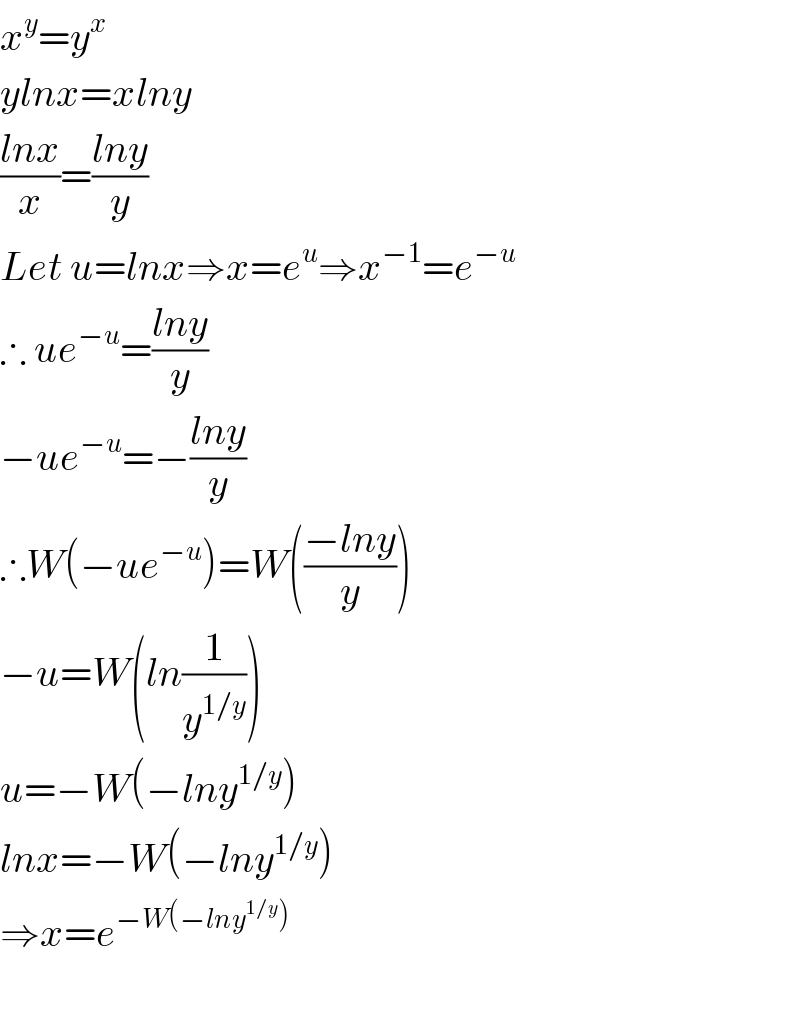
$${x}^{{y}} ={y}^{{x}} \\ $$$${ylnx}={xlny} \\ $$$$\frac{{lnx}}{{x}}=\frac{{lny}}{{y}} \\ $$$${Let}\:{u}={lnx}\Rightarrow{x}={e}^{{u}} \Rightarrow{x}^{−\mathrm{1}} ={e}^{−{u}} \\ $$$$\therefore\:{ue}^{−{u}} =\frac{{lny}}{{y}} \\ $$$$−{ue}^{−{u}} =−\frac{{lny}}{{y}} \\ $$$$\therefore{W}\left(−{ue}^{−{u}} \right)={W}\left(\frac{−{lny}}{{y}}\right) \\ $$$$−{u}={W}\left({ln}\frac{\mathrm{1}}{{y}^{\mathrm{1}/{y}} }\right) \\ $$$${u}=−{W}\left(−{lny}^{\mathrm{1}/{y}} \right) \\ $$$${lnx}=−{W}\left(−{lny}^{\mathrm{1}/{y}} \right) \\ $$$$\Rightarrow{x}={e}^{−{W}\left(−{lny}^{\mathrm{1}/{y}} \right)} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 03/Aug/16

$${Thanks}\:{so}\:{much} \\ $$
