
Question Number 69130 by Cmr 237 last updated on 21/Sep/19
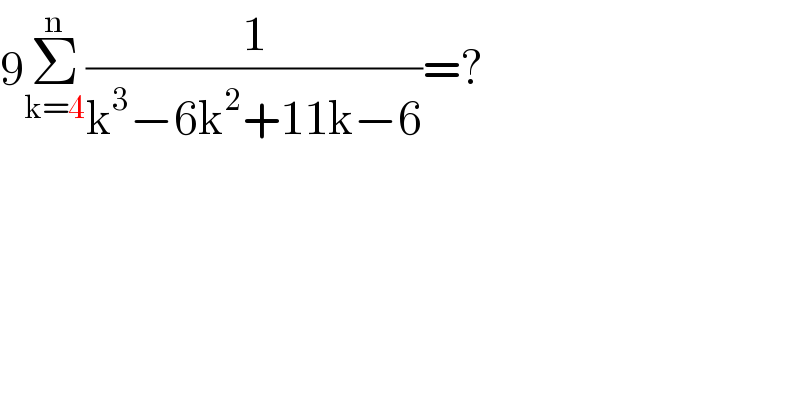
$$\mathrm{9}\underset{\mathrm{k}=\mathrm{4}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} −\mathrm{6k}^{\mathrm{2}} +\mathrm{11k}−\mathrm{6}}=? \\ $$$$\:\:\:\:\: \\ $$
Commented by Henri Boucatchou last updated on 20/Sep/19

$$\:\:\boldsymbol{\mathrm{Please}}\:\:\boldsymbol{\mathrm{check}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{question}}\:\:\boldsymbol{\mathrm{once}}\:\:\boldsymbol{\mathrm{more}}\:\:\left(\boldsymbol{\mathrm{where}}\:\:\boldsymbol{\mathrm{k}}\:\:\boldsymbol{\mathrm{stats}}\:\:\boldsymbol{\mathrm{from}}\:\:\boldsymbol{\mathrm{in}}\:\:\underset{\boldsymbol{\mathrm{k}}=?} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{because}}\:\:\boldsymbol{\mathrm{k}}^{\mathrm{3}} −\:\mathrm{6}\boldsymbol{\mathrm{k}}^{\mathrm{2}} \:+\:\mathrm{11}\boldsymbol{\mathrm{k}}\:−\:\mathrm{6}\:=\:\left(\boldsymbol{\mathrm{k}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{k}}−\mathrm{2}\right)\left(\boldsymbol{\mathrm{k}}−\mathrm{3}\right),\:\:\boldsymbol{\mathrm{therefore}}\:\:\boldsymbol{\mathrm{k}}\:\:\boldsymbol{\mathrm{can}}'\boldsymbol{\mathrm{t}}\:\:\boldsymbol{\mathrm{take}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{values}}\:\:\mathrm{1},\:\mathrm{2},\:\mathrm{3}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{note}}\:\:\boldsymbol{\mathrm{that}}\:\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}^{\mathrm{3}} \:−\:\mathrm{6}\boldsymbol{\mathrm{k}}^{\mathrm{2}} \:+\:\mathrm{11}\boldsymbol{\mathrm{k}}\:−\:\mathrm{6}}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\boldsymbol{\mathrm{k}}\:−\:\mathrm{1}}\:−\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}\:−\:\mathrm{2}}\:+\:\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\boldsymbol{\mathrm{k}}\:−\:\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 20/Sep/19

$${i}\:{suppose}\:{that}\:{the}\:{decomposition}\:{is}\:{correct}\:\left({i}\:{dont}\:{verfy}\:{it}\right) \\ $$$$\Rightarrow{let}\:{S}_{{n}} =\sum_{{k}=\mathrm{4}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{3}} −\mathrm{6}{k}^{\mathrm{2}} \:+\mathrm{11}{k}−\mathrm{6}}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}−\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{3}} \\ $$$$\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{2}}\:=\sum_{{k}=\mathrm{2}} ^{{n}−\mathrm{2}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}−\mathrm{2}} −\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:=\sum_{{k}=\mathrm{3}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}−\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:={H}_{{n}−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\sum_{{k}=\mathrm{4}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{3}}\:=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{3}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}−\mathrm{3}} \:\Rightarrow \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{4}}\:−{H}_{{n}−\mathrm{2}} +\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}−\mathrm{3}} \:\Rightarrow \\ $$$${S}_{{n}} \sim\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{ln}\left({n}−\mathrm{1}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)+{ln}\left({n}−\mathrm{3}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}−\mathrm{3}}\right)\right) \\ $$$$−{ln}\left({n}−\mathrm{2}\right)−\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}−\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}_{{n}} \sim{ln}\sqrt{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{3}\right)}\:\:−{ln}\left({n}−\mathrm{2}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}{o}\left(\frac{\mathrm{1}}{{n}−\mathrm{3}}\right)\:\Rightarrow \\ $$$${S}_{{n}} \sim{ln}\left(\frac{\sqrt{{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{3}}}{{n}−\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\mathrm{9}{S}_{{n}} =\frac{\mathrm{9}}{\mathrm{4}}\:\:\:\:\left(\gamma\:{is}\:{the}\:{constant}\:{of}\:{euler}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 20/Sep/19
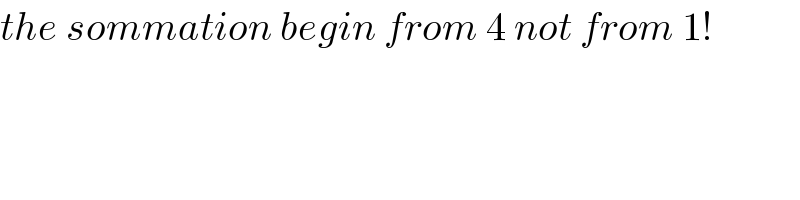
$${the}\:{sommation}\:{begin}\:{from}\:\mathrm{4}\:{not}\:{from}\:\mathrm{1}! \\ $$
