
Question Number 69092 by Mr. K last updated on 19/Sep/19

Answered by mr W last updated on 21/Sep/19
Commented by mr W last updated on 21/Sep/19
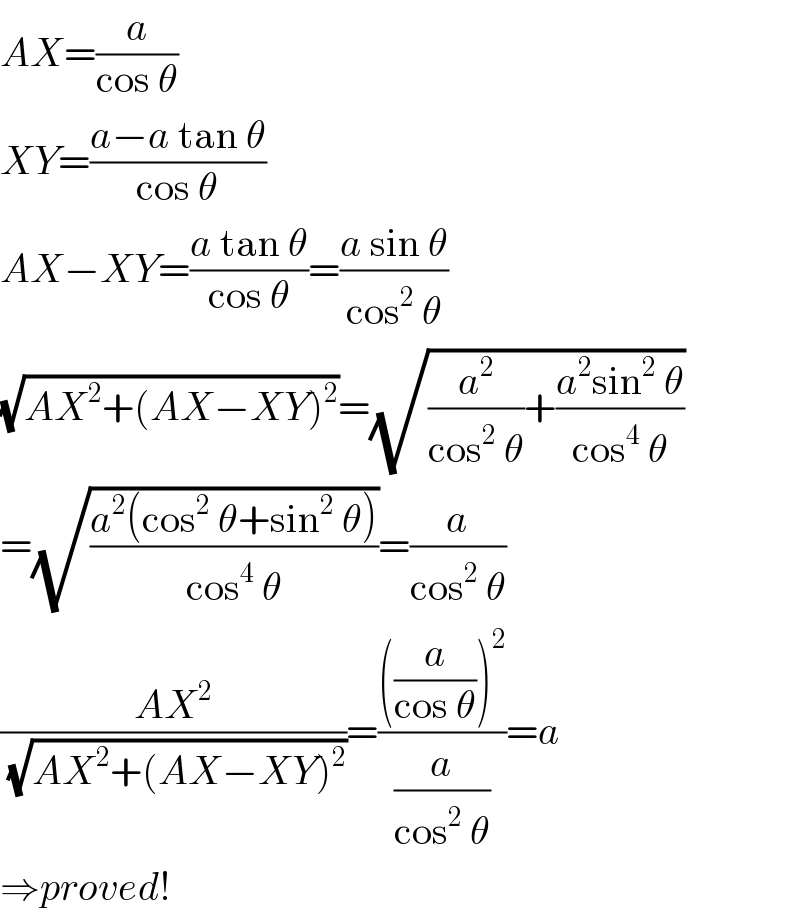
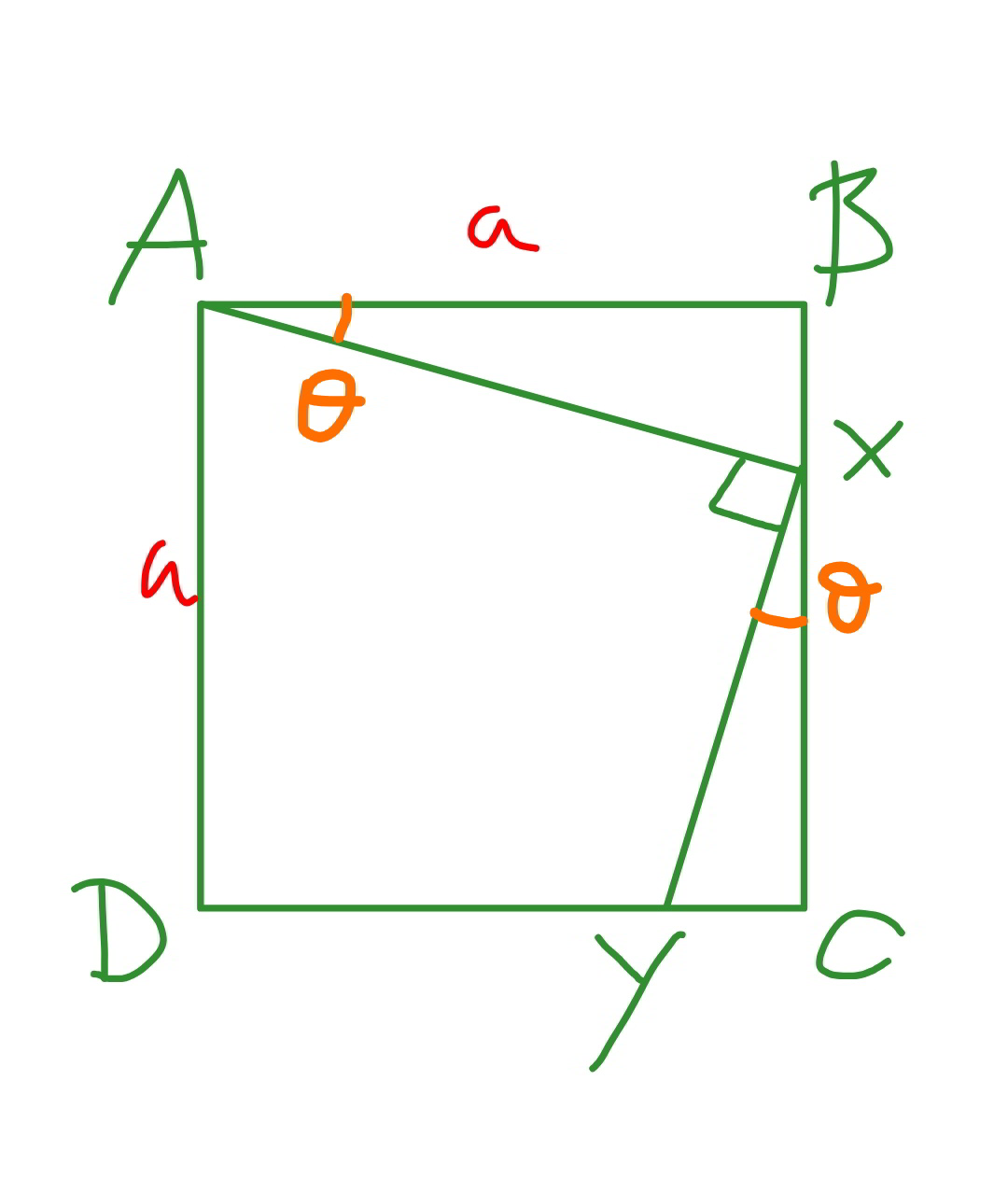
$${AX}=\frac{{a}}{\mathrm{cos}\:\theta} \\ $$$${XY}=\frac{{a}−{a}\:\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta} \\ $$$${AX}−{XY}=\frac{{a}\:\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta}=\frac{{a}\:\mathrm{sin}\:\theta}{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\sqrt{{AX}^{\mathrm{2}} +\left({AX}−{XY}\right)^{\mathrm{2}} }=\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta}+\frac{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{cos}^{\mathrm{4}} \:\theta}} \\ $$$$=\sqrt{\frac{{a}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta\right)}{\mathrm{cos}^{\mathrm{4}} \:\theta}}=\frac{{a}}{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\frac{{AX}^{\mathrm{2}} }{\sqrt{{AX}^{\mathrm{2}} +\left({AX}−{XY}\right)^{\mathrm{2}} }}=\frac{\left(\frac{{a}}{\mathrm{cos}\:\theta}\right)^{\mathrm{2}} }{\frac{{a}}{\mathrm{cos}^{\mathrm{2}} \:\theta}}={a} \\ $$$$\Rightarrow{proved}! \\ $$
Commented by TawaTawa last updated on 21/Sep/19

$$\mathrm{Wow},\:\mathrm{nice}\:\mathrm{sir} \\ $$
Commented by Mr. K last updated on 21/Sep/19
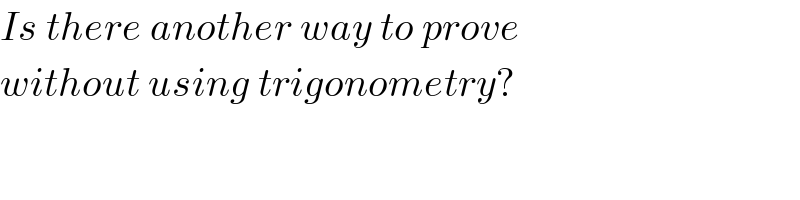
$${Is}\:{there}\:{another}\:{way}\:{to}\:{prove} \\ $$$${without}\:{using}\:{trigonometry}? \\ $$
Commented by mr W last updated on 22/Sep/19
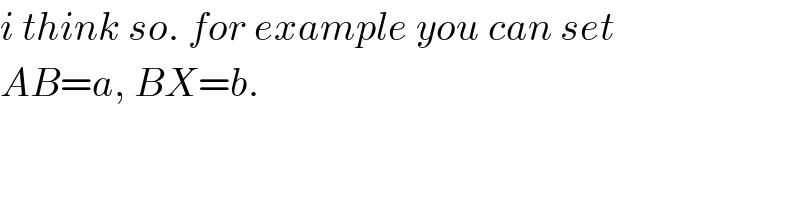
$${i}\:{think}\:{so}.\:{for}\:{example}\:{you}\:{can}\:{set} \\ $$$${AB}={a},\:{BX}={b}. \\ $$
