
Question Number 69045 by jagannath19 last updated on 18/Sep/19
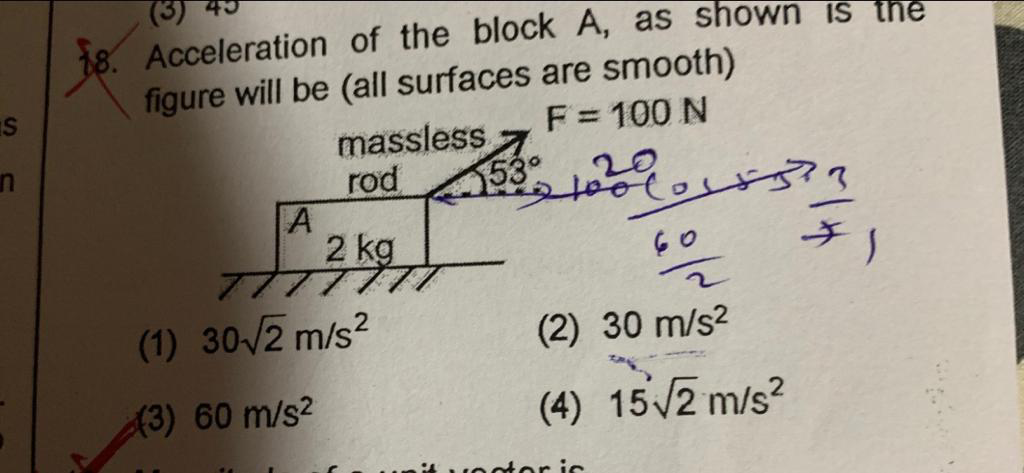
Answered by Rio Michael last updated on 18/Sep/19

$${F}_{{net}} =\:\mathrm{100}{cos}\mathrm{53}° \\ $$$${ma}\:\approx\:\mathrm{60} \\ $$$$\mathrm{2}\left({a}\right)\:=\:\mathrm{60} \\ $$$${a}\:=\:\mathrm{30}{m}/{s}^{\mathrm{2}} \\ $$
Answered by mr W last updated on 18/Sep/19
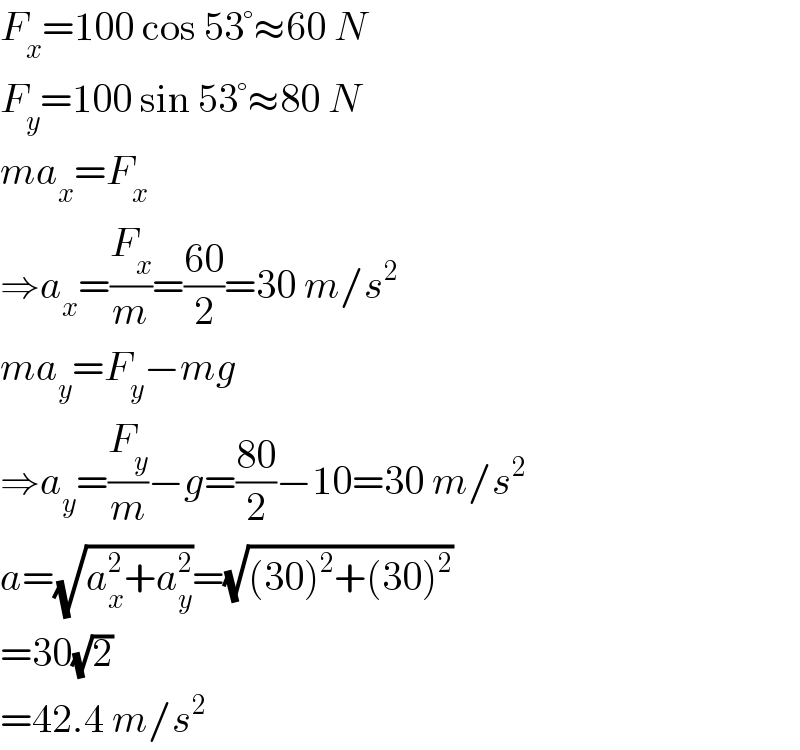
$${F}_{{x}} =\mathrm{100}\:\mathrm{cos}\:\mathrm{53}°\approx\mathrm{60}\:{N} \\ $$$${F}_{{y}} =\mathrm{100}\:\mathrm{sin}\:\mathrm{53}°\approx\mathrm{80}\:{N} \\ $$$${ma}_{{x}} ={F}_{{x}} \\ $$$$\Rightarrow{a}_{{x}} =\frac{{F}_{{x}} }{{m}}=\frac{\mathrm{60}}{\mathrm{2}}=\mathrm{30}\:{m}/{s}^{\mathrm{2}} \\ $$$${ma}_{{y}} ={F}_{{y}} −{mg} \\ $$$$\Rightarrow{a}_{{y}} =\frac{{F}_{{y}} }{{m}}−{g}=\frac{\mathrm{80}}{\mathrm{2}}−\mathrm{10}=\mathrm{30}\:{m}/{s}^{\mathrm{2}} \\ $$$${a}=\sqrt{{a}_{{x}} ^{\mathrm{2}} +{a}_{{y}} ^{\mathrm{2}} }=\sqrt{\left(\mathrm{30}\right)^{\mathrm{2}} +\left(\mathrm{30}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{30}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{42}.\mathrm{4}\:{m}/{s}^{\mathrm{2}} \\ $$
Commented by necxxx last updated on 19/Sep/19
$${wow}.{Thank}\:{you}\:{so}\:{much} \\ $$
