
Question Number 69034 by ahmadshah last updated on 18/Sep/19
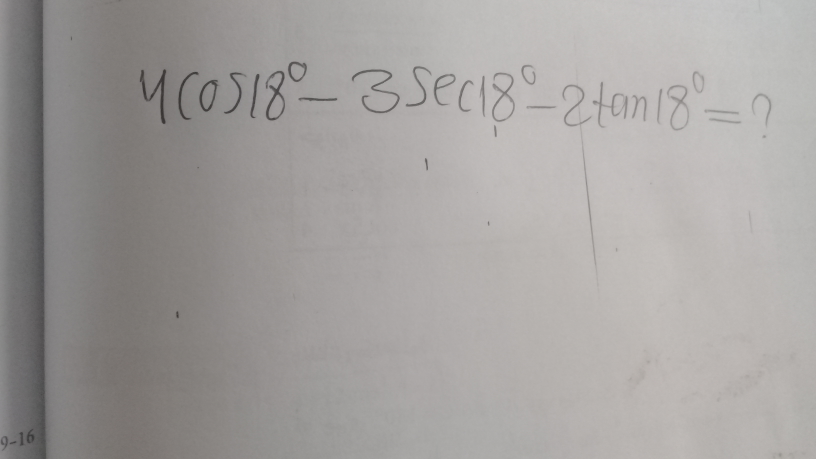
Answered by $@ty@m123 last updated on 18/Sep/19

$$\mathrm{4cos}\:{x}−\mathrm{3sec}\:{x}−\mathrm{2tan}\:{x} \\ $$$$\mathrm{4cos}\:{x}−\frac{\mathrm{3}}{\mathrm{cos}\:{x}}−\frac{\mathrm{2sin}\:{x}}{\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{4cos}\:^{\mathrm{2}} {x}−\mathrm{3}−\mathrm{2sin}\:{x}}{\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}−\mathrm{2sin}\:{x}\mathrm{cos}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$=\frac{\mathrm{cos}\:\mathrm{3}{x}−\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$=\frac{\mathrm{cos}\:\mathrm{54}−\mathrm{sin}\:\mathrm{36}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{18}} \\ $$$$=\frac{\mathrm{cos}\:\mathrm{54}−\mathrm{cos}\:\mathrm{54}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{18}} \\ $$$$=\mathrm{0} \\ $$
Answered by MJS last updated on 18/Sep/19

$$\mathrm{sin}\:\mathrm{18}°\:=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\mathrm{18}°\:=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{sec}\:\mathrm{18}°\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}};\:\mathrm{tan}\:\mathrm{18}°\:=\frac{\left(−\mathrm{1}+\sqrt{\mathrm{5}}\right)\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}} \\ $$$$\mathrm{4}\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}−\mathrm{3}\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}}−\mathrm{2}\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}}= \\ $$$$=\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}−\frac{\mathrm{6}\sqrt{\mathrm{2}}+\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)\sqrt{\mathrm{2}}}{\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}}= \\ $$$$=\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}−\frac{\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)\sqrt{\mathrm{2}}}{\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}}= \\ $$$$=\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}\sqrt{\mathrm{2}}= \\ $$$$=\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}−\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}=\mathrm{0} \\ $$
