
Previous in Differential Equation Next in Differential Equation
Question Number 68946 by ramirez105 last updated on 17/Sep/19
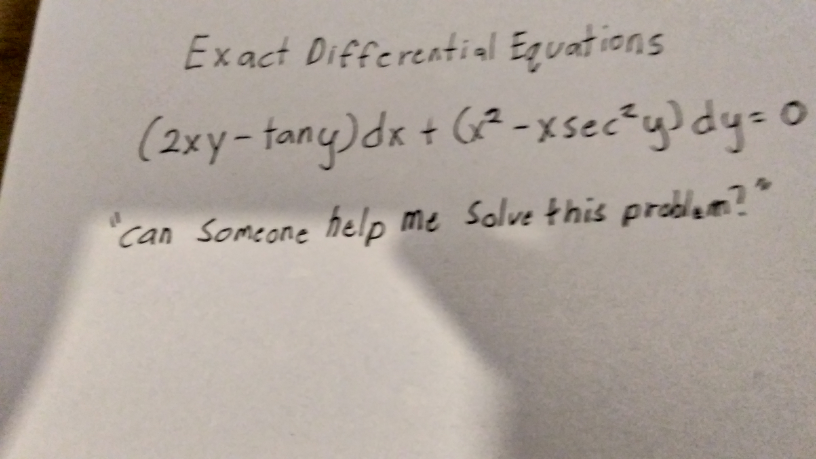
Commented by kaivan.ahmadi last updated on 17/Sep/19
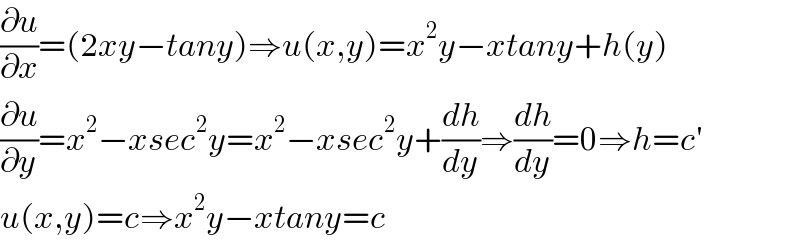
$$\frac{\partial{u}}{\partial{x}}=\left(\mathrm{2}{xy}−{tany}\right)\Rightarrow{u}\left({x},{y}\right)={x}^{\mathrm{2}} {y}−{xtany}+{h}\left({y}\right) \\ $$$$\frac{\partial{u}}{\partial{y}}={x}^{\mathrm{2}} −{xsec}^{\mathrm{2}} {y}={x}^{\mathrm{2}} −{xsec}^{\mathrm{2}} {y}+\frac{{dh}}{{dy}}\Rightarrow\frac{{dh}}{{dy}}=\mathrm{0}\Rightarrow{h}={c}' \\ $$$${u}\left({x},{y}\right)={c}\Rightarrow{x}^{\mathrm{2}} {y}−{xtany}={c} \\ $$
