
Question Number 6890 by Tawakalitu. last updated on 01/Aug/16
Commented by Yozzii last updated on 02/Aug/16
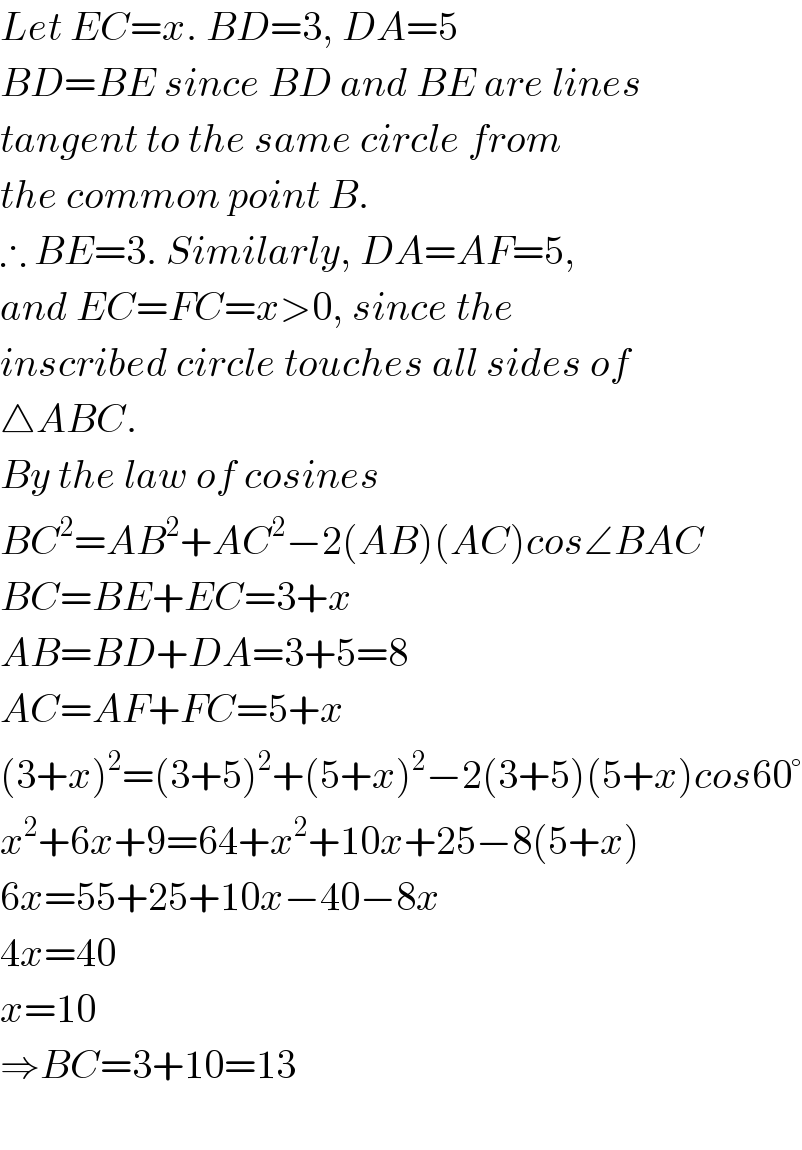
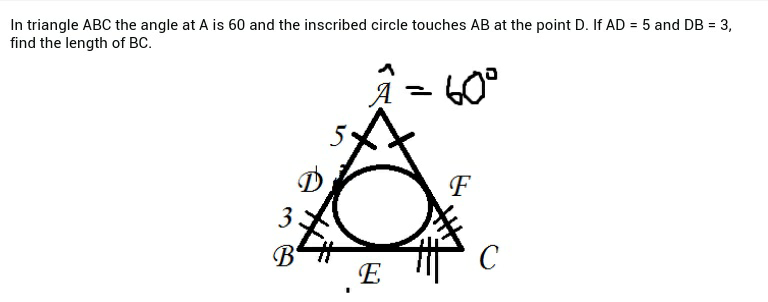
$${Let}\:{EC}={x}.\:{BD}=\mathrm{3},\:{DA}=\mathrm{5} \\ $$$${BD}={BE}\:{since}\:{BD}\:{and}\:{BE}\:{are}\:{lines} \\ $$$${tangent}\:{to}\:{the}\:{same}\:{circle}\:{from}\: \\ $$$${the}\:{common}\:{point}\:{B}. \\ $$$$\therefore\:{BE}=\mathrm{3}.\:{Similarly},\:{DA}={AF}=\mathrm{5}, \\ $$$${and}\:{EC}={FC}={x}>\mathrm{0},\:{since}\:{the}\: \\ $$$${inscribed}\:{circle}\:{touches}\:{all}\:{sides}\:{of} \\ $$$$\bigtriangleup{ABC}. \\ $$$${By}\:{the}\:{law}\:{of}\:{cosines} \\ $$$${BC}^{\mathrm{2}} ={AB}^{\mathrm{2}} +{AC}^{\mathrm{2}} −\mathrm{2}\left({AB}\right)\left({AC}\right){cos}\angle{BAC} \\ $$$${BC}={BE}+{EC}=\mathrm{3}+{x} \\ $$$${AB}={BD}+{DA}=\mathrm{3}+\mathrm{5}=\mathrm{8} \\ $$$${AC}={AF}+{FC}=\mathrm{5}+{x} \\ $$$$\left(\mathrm{3}+{x}\right)^{\mathrm{2}} =\left(\mathrm{3}+\mathrm{5}\right)^{\mathrm{2}} +\left(\mathrm{5}+{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}+\mathrm{5}\right)\left(\mathrm{5}+{x}\right){cos}\mathrm{60}° \\ $$$${x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9}=\mathrm{64}+{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{25}−\mathrm{8}\left(\mathrm{5}+{x}\right) \\ $$$$\mathrm{6}{x}=\mathrm{55}+\mathrm{25}+\mathrm{10}{x}−\mathrm{40}−\mathrm{8}{x} \\ $$$$\mathrm{4}{x}=\mathrm{40} \\ $$$${x}=\mathrm{10} \\ $$$$\Rightarrow{BC}=\mathrm{3}+\mathrm{10}=\mathrm{13} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 02/Aug/16
$${Wow},\:{i}\:{really}\:{appreciate}.\:{Thanks}\:{so}\:{much}. \\ $$
