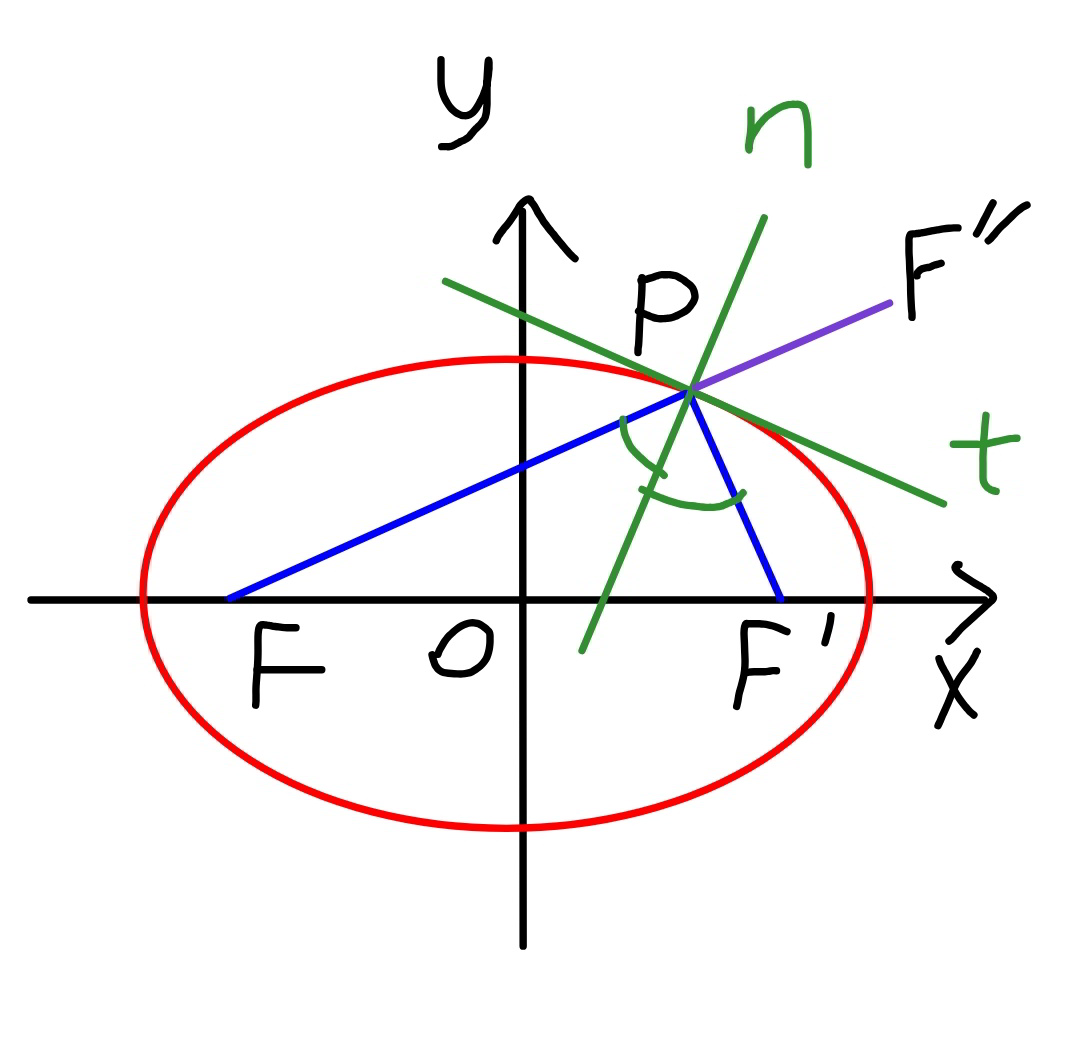
Question Number 68783 by peter frank last updated on 15/Sep/19

Commented by peter frank last updated on 22/Sep/19

$${thank}\:{you}\: \\ $$
Commented by ajfour last updated on 15/Sep/19
Commented by peter frank last updated on 21/Sep/19
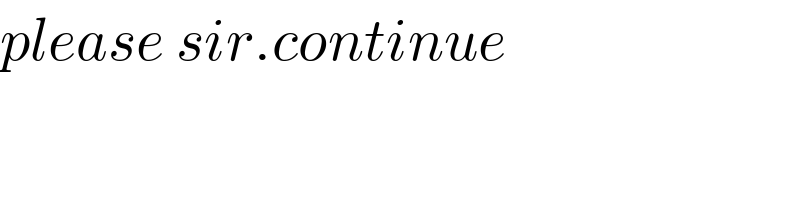
$${please}\:{sir}.{continue} \\ $$
Commented by ajfour last updated on 21/Sep/19

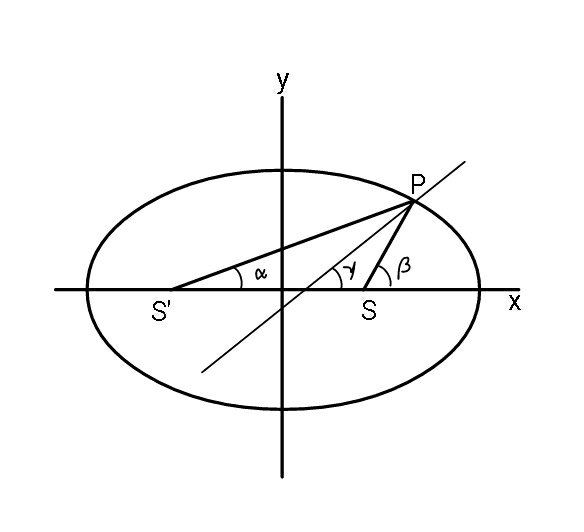
$${let}\:{S}\:'{P}\:={a}+{s}\:,\:\:\:{SP}\:=\:{a}−{s} \\ $$$${let}\:{P}\:\left({h},{k}\right) \\ $$$$\:\:\:\:\frac{{S}\:'{P}}{{SP}}=\frac{{a}+{s}}{{a}−{s}} \\ $$$${a}−{s}={e}\left(\frac{{a}}{{e}}−{h}\right) \\ $$$${a}+{s}={e}\left(\frac{{a}}{{e}}+{h}\right) \\ $$$$\Rightarrow\:{s}={eh} \\ $$$$\:\:\:\frac{{S}\:'{P}}{{SP}}=\frac{{a}+{eh}}{{a}−{eh}}\:\:\:\:\:\:\:\:\:................\left({i}\right) \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\Rightarrow\:\:−\frac{{dx}}{{dy}}=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{y}}{{x}}\right) \\ $$$${slope}\:{of}\:{normal} \\ $$$$\:\:\:=−\frac{{dx}}{{dy}}\mid_{{P}} =\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{k}}{{h}}\right) \\ $$$$\:\:\:\:\:{eq}.\:{of}\:{normal} \\ $$$${y}−{k}=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{k}}{{h}}\right)\left({x}−{h}\right) \\ $$$${let}\:{normal}\:{intersect}\:{x}-{axis} \\ $$$${at}\:{N}\left(\mathrm{0},\:{x}_{{int}} \right) \\ $$$${x}_{{int}} ={h}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\frac{{SN}}{{S}\:'{N}}=\frac{{ae}−{x}_{{int}} }{{x}_{{int}} +{ae}}=\frac{{ae}−{h}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}{{h}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)+{ae}}={r}_{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{SN}}{{S}\:'{N}}=\frac{{a}−{eh}}{{eh}+{a}}\:\:\:\:\:\:\:\:.............\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{find} \\ $$$$\:\:\:\:\:\:\frac{{S}\:'{P}}{{SP}}=\frac{{S}\:'{N}}{{SN}} \\ $$$$\Rightarrow\:\:{PN}\:{is}\:{angular}\:{bisector} \\ $$$$\:\:\:\:\:\:{of}\:\angle{S}\:'{PS}\:. \\ $$
Commented by peter frank last updated on 22/Sep/19

$${please}\:{help}\:\mathrm{69230} \\ $$
Answered by mr W last updated on 15/Sep/19