
Question Number 68768 by aliesam last updated on 15/Sep/19
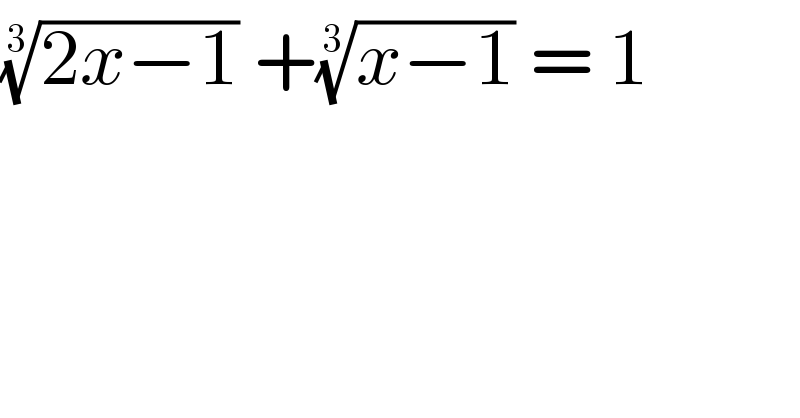
$$\sqrt[{\mathrm{3}}]{\mathrm{2}{x}−\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}−\mathrm{1}}\:=\:\mathrm{1} \\ $$
Commented by kaivan.ahmadi last updated on 15/Sep/19
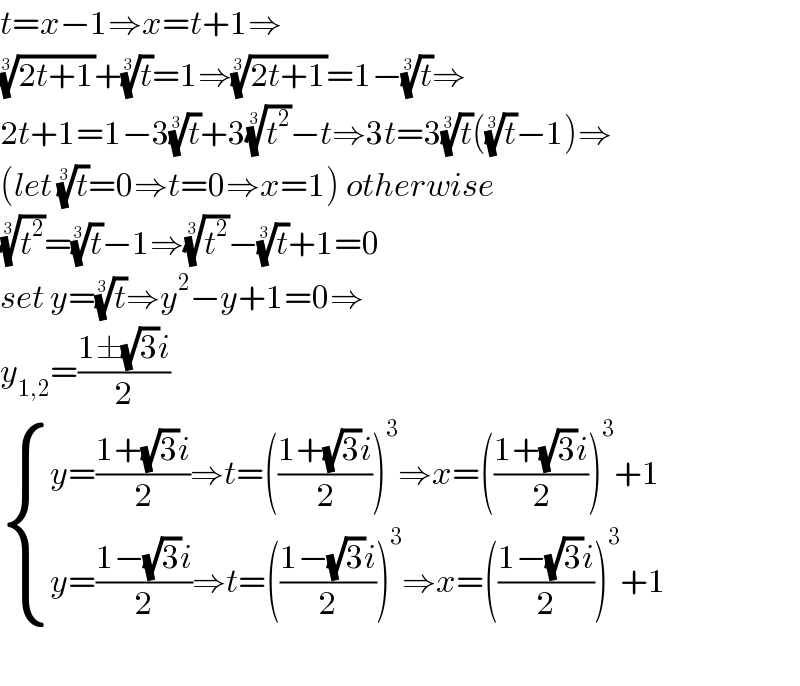
$${t}={x}−\mathrm{1}\Rightarrow{x}={t}+\mathrm{1}\Rightarrow \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}{t}+\mathrm{1}}+\sqrt[{\mathrm{3}}]{{t}}=\mathrm{1}\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{2}{t}+\mathrm{1}}=\mathrm{1}−\sqrt[{\mathrm{3}}]{{t}}\Rightarrow \\ $$$$\mathrm{2}{t}+\mathrm{1}=\mathrm{1}−\mathrm{3}\sqrt[{\mathrm{3}}]{{t}}+\mathrm{3}\sqrt[{\mathrm{3}}]{{t}^{\mathrm{2}} }−{t}\Rightarrow\mathrm{3}{t}=\mathrm{3}\sqrt[{\mathrm{3}}]{{t}}\left(\sqrt[{\mathrm{3}}]{{t}}−\mathrm{1}\right)\Rightarrow \\ $$$$\left({let}\:\sqrt[{\mathrm{3}}]{{t}}=\mathrm{0}\Rightarrow{t}=\mathrm{0}\Rightarrow{x}=\mathrm{1}\right)\:{otherwise} \\ $$$$\sqrt[{\mathrm{3}}]{{t}^{\mathrm{2}} }=\sqrt[{\mathrm{3}}]{{t}}−\mathrm{1}\Rightarrow\sqrt[{\mathrm{3}}]{{t}^{\mathrm{2}} }−\sqrt[{\mathrm{3}}]{{t}}+\mathrm{1}=\mathrm{0} \\ $$$${set}\:{y}=\sqrt[{\mathrm{3}}]{{t}}\Rightarrow{y}^{\mathrm{2}} −{y}+\mathrm{1}=\mathrm{0}\Rightarrow \\ $$$${y}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}{i}}{\mathrm{2}} \\ $$$$\begin{cases}{{y}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\Rightarrow{t}=\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{3}} \Rightarrow{x}=\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{3}} +\mathrm{1}}\\{{y}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\Rightarrow{t}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{3}} \Rightarrow{x}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{3}} +\mathrm{1}}\end{cases} \\ $$$$ \\ $$
Answered by MJS last updated on 16/Sep/19
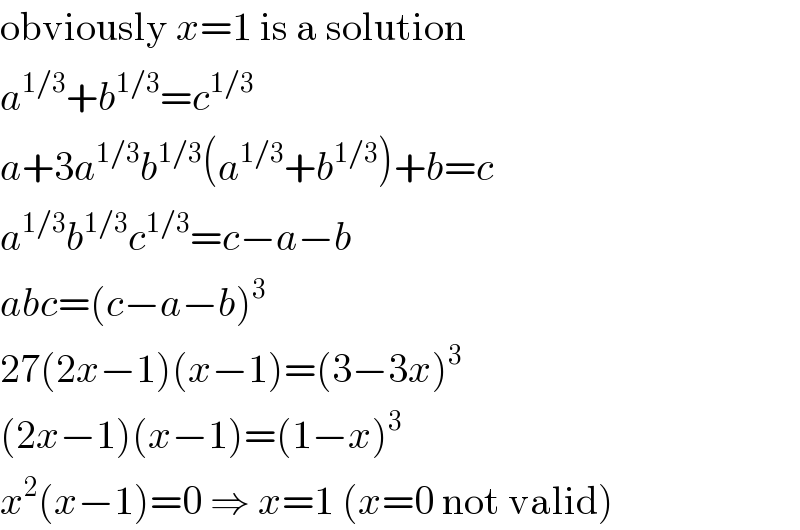
$$\mathrm{obviously}\:{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$${a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} ={c}^{\mathrm{1}/\mathrm{3}} \\ $$$${a}+\mathrm{3}{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} \left({a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} \right)+{b}={c} \\ $$$${a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} {c}^{\mathrm{1}/\mathrm{3}} ={c}−{a}−{b} \\ $$$${abc}=\left({c}−{a}−{b}\right)^{\mathrm{3}} \\ $$$$\mathrm{27}\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)=\left(\mathrm{3}−\mathrm{3}{x}\right)^{\mathrm{3}} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)=\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{1}\:\left({x}=\mathrm{0}\:\mathrm{not}\:\mathrm{valid}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 16/Sep/19
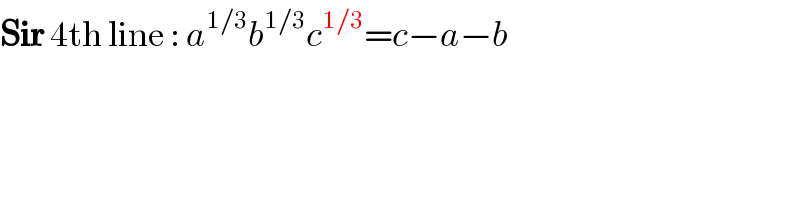
$$\boldsymbol{\mathrm{Sir}}\:\mathrm{4th}\:\mathrm{line}\::\:{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} {c}^{\mathrm{1}/\mathrm{3}} ={c}−{a}−{b} \\ $$$$ \\ $$
Commented by MJS last updated on 16/Sep/19
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$
