
Question Number 68666 by ahmadshah last updated on 14/Sep/19
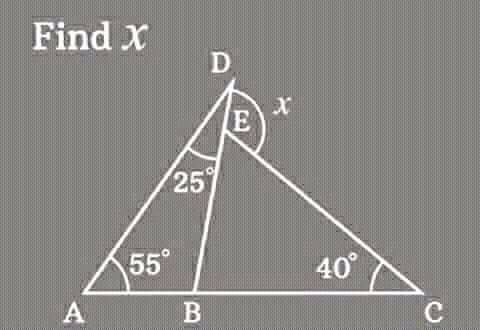
Commented by mr W last updated on 14/Sep/19
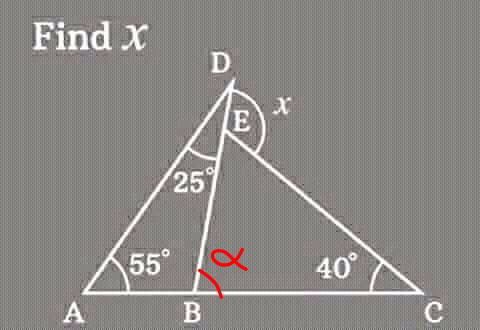
Commented by mr W last updated on 14/Sep/19
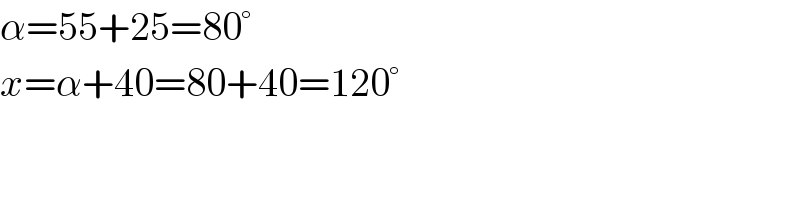
$$\alpha=\mathrm{55}+\mathrm{25}=\mathrm{80}° \\ $$$${x}=\alpha+\mathrm{40}=\mathrm{80}+\mathrm{40}=\mathrm{120}° \\ $$
Answered by ahmadshah last updated on 14/Sep/19
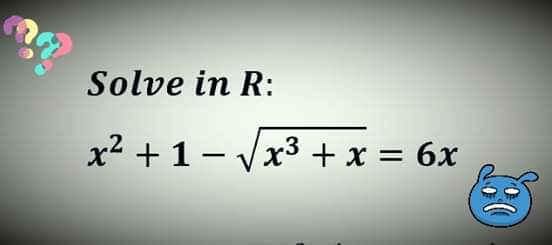
Commented by ahmadshah last updated on 14/Sep/19

$$ \\ $$
Commented by Prithwish sen last updated on 15/Sep/19
$$\mathrm{You}\:\mathrm{have}\:\mathrm{a}\:\mathrm{creative}\:\mathrm{mind}.\mathrm{Thanks}\:\mathrm{rasheed}\:\mathrm{Sir}. \\ $$
Commented by Prithwish sen last updated on 16/Sep/19

$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{3}\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}\:\:−\mathrm{6x}\:=\mathrm{0} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{3}\sqrt{\mathrm{x}}\right)+\mathrm{2}\sqrt{\mathrm{x}}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:−\:\mathrm{3}\sqrt{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{2}\sqrt{\mathrm{x}}\right)\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{3}\sqrt{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\therefore\:\boldsymbol{\mathrm{either}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{or}} \\ $$$$\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:+\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{3}\sqrt{\boldsymbol{\mathrm{x}}}\:=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{x}}\:+\mathrm{1}\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:−\mathrm{9}\boldsymbol{\mathrm{x}}\:+\mathrm{1}\:=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{x}}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{9}\pm\sqrt{\mathrm{81}−\mathrm{4}}}{\mathrm{2}}\:\:\:\: \\ $$$$\therefore\mathrm{x}=\:\mathrm{2}\pm\sqrt{\mathrm{3}}\:\:,\:\:\frac{\mathrm{9}\pm\sqrt{\mathrm{77}}}{\mathrm{2}}\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by Rasheed.Sindhi last updated on 15/Sep/19
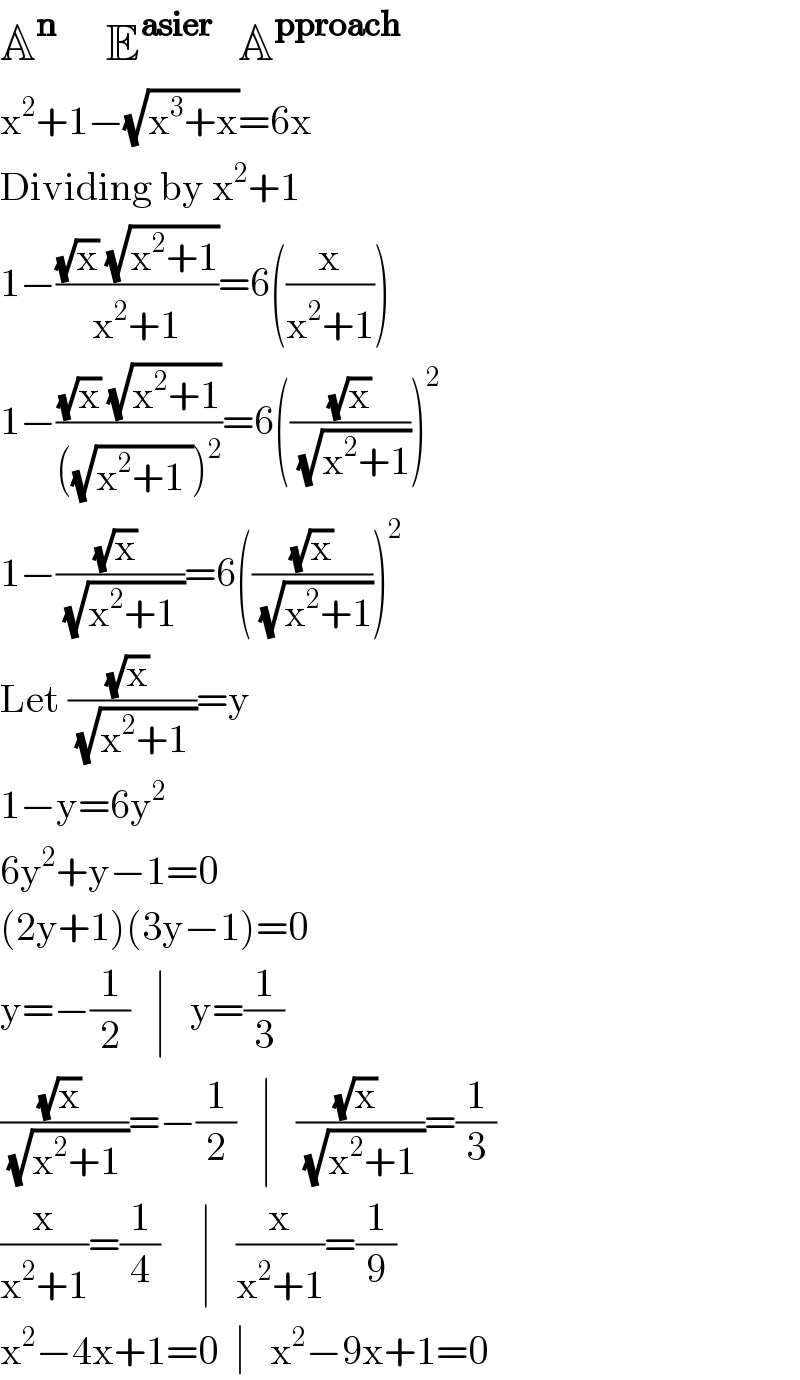
$$\mathbb{A}^{\boldsymbol{\mathrm{n}}} \:\:\:\:\:\mathbb{E}^{\boldsymbol{\mathrm{asier}}\:} \:\:\mathbb{A}^{\boldsymbol{\mathrm{pproach}}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{x}}=\mathrm{6x} \\ $$$$\mathrm{Dividing}\:\mathrm{by}\:\mathrm{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{1}−\frac{\sqrt{\mathrm{x}}\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{6}\left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\mathrm{1}−\frac{\sqrt{\mathrm{x}}\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:}\right)^{\mathrm{2}} }=\mathrm{6}\left(\frac{\sqrt{\mathrm{x}}}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−\frac{\sqrt{\mathrm{x}}\:}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:}}=\mathrm{6}\left(\frac{\sqrt{\mathrm{x}}}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{Let}\:\frac{\sqrt{\mathrm{x}}\:}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:}}=\mathrm{y} \\ $$$$\mathrm{1}−\mathrm{y}=\mathrm{6y}^{\mathrm{2}} \\ $$$$\mathrm{6y}^{\mathrm{2}} +\mathrm{y}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2y}+\mathrm{1}\right)\left(\mathrm{3y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{y}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\mid\:\:\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\sqrt{\mathrm{x}}\:}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\mid\:\:\:\frac{\sqrt{\mathrm{x}}\:}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\mid\:\:\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}=\mathrm{0}\:\:\mid\:\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{9x}+\mathrm{1}=\mathrm{0} \\ $$
Commented by Prithwish sen last updated on 15/Sep/19

$$\mathrm{Excellent}\:\mathrm{Sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 15/Sep/19

$$\boldsymbol{\mathrm{Sir}},\:\mathrm{actually}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{raised}\:\mathrm{in} \\ $$$$\mathrm{my}\:\mathrm{mind}\:\mathrm{after}\:\mathrm{seeing}\:\mathrm{your}\:\mathrm{solution}. \\ $$$$\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{solution}! \\ $$
Commented by mind is power last updated on 15/Sep/19
![x=tg(t)..x≥0⇒t∈[0,(π/2)] ⇒(1/(cos^2 (t)))−(√((sin(t))/(cos^3 (t))))=6((sin(t))/(cos(t))) ⇒1−(√(sin(t)cos(t)))=6sin(t)cos(t) ⇒1−(√((sin(2t))/2))=3sin(2t) ⇒(√(sin(2t) )) solution of 1−(X/(√2))=3X^2](Q68784.png)
$${x}={tg}\left({t}\right)..{x}\geqslant\mathrm{0}\Rightarrow{t}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Rightarrow\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({t}\right)}−\sqrt{\frac{{sin}\left({t}\right)}{{cos}^{\mathrm{3}} \left({t}\right)}}=\mathrm{6}\frac{{sin}\left({t}\right)}{{cos}\left({t}\right)} \\ $$$$ \\ $$$$\Rightarrow\mathrm{1}−\sqrt{{sin}\left({t}\right){cos}\left({t}\right)}=\mathrm{6}{sin}\left({t}\right){cos}\left({t}\right) \\ $$$$\Rightarrow\mathrm{1}−\sqrt{\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}=\mathrm{3}{sin}\left(\mathrm{2}{t}\right) \\ $$$$\Rightarrow\sqrt{{sin}\left(\mathrm{2}{t}\right)\:}\:\:{solution}\:{of}\:\mathrm{1}−\frac{{X}}{\sqrt{\mathrm{2}}}=\mathrm{3}{X}^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Sep/19

$${Sir}\:{mind}-{is}-{power},{Nice}\:{idea}\:{of} \\ $$$${connecting}\:{the}\:{algebraic}\:{problem} \\ $$$${to}\:{trigonom}\mathrm{etry}! \\ $$
