
Question Number 68618 by Rio Michael last updated on 14/Sep/19

$${solve}\:{for}\:{x}\:{the}\:{following}\:{equations} \\ $$$$\left.{a}\right)\:{log}\:{x}^{\mathrm{3}} \:−\:\mathrm{2}{log}\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{log}\:{x}\:\:+\:\mathrm{2}{log}\:\sqrt{{x}}\:=\:\mathrm{3} \\ $$$$\left.{b}\right)\:{log}_{{x}} \mathrm{24}\:−\mathrm{3}{log}_{{x}} \mathrm{4}\:\:+\:\mathrm{2}{log}_{{x}} \mathrm{3}\:=−\mathrm{3} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Sep/19
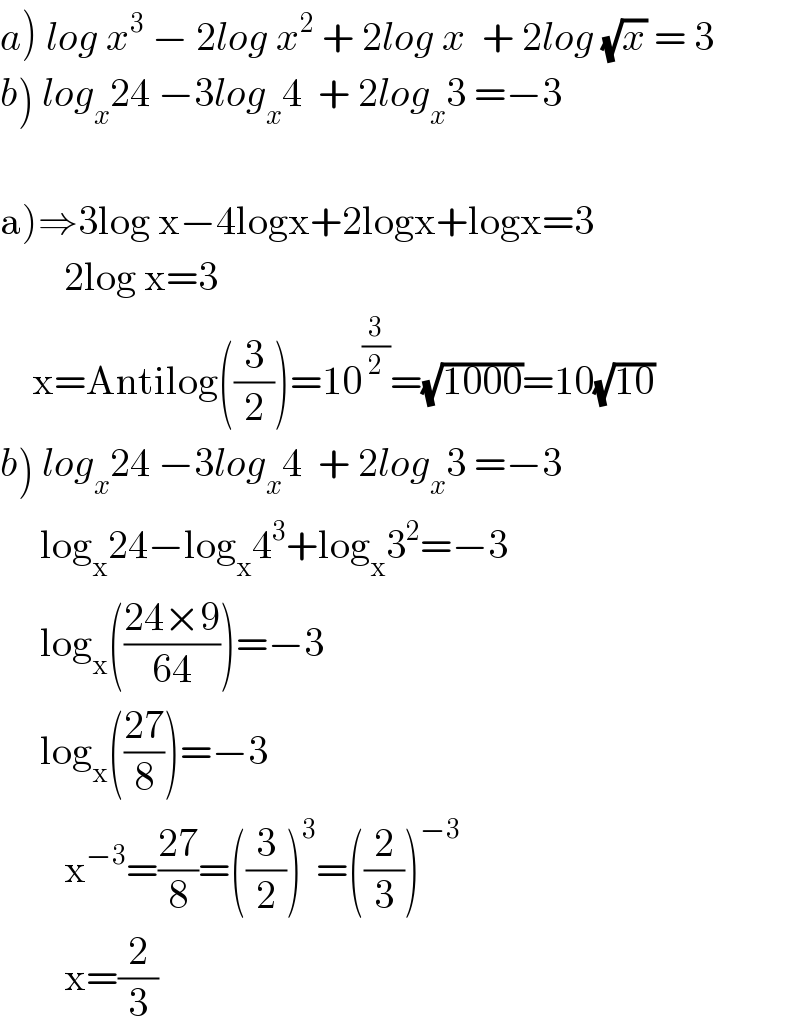
$$\left.{a}\right)\:{log}\:{x}^{\mathrm{3}} \:−\:\mathrm{2}{log}\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{log}\:{x}\:\:+\:\mathrm{2}{log}\:\sqrt{{x}}\:=\:\mathrm{3} \\ $$$$\left.{b}\right)\:{log}_{{x}} \mathrm{24}\:−\mathrm{3}{log}_{{x}} \mathrm{4}\:\:+\:\mathrm{2}{log}_{{x}} \mathrm{3}\:=−\mathrm{3} \\ $$$$\:\:\: \\ $$$$\left.\mathrm{a}\right)\Rightarrow\mathrm{3log}\:\mathrm{x}−\mathrm{4logx}+\mathrm{2logx}+\mathrm{logx}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2log}\:\mathrm{x}=\mathrm{3} \\ $$$$\:\:\:\:\mathrm{x}=\mathrm{Antilog}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{10}^{\frac{\mathrm{3}}{\mathrm{2}}} =\sqrt{\mathrm{1000}}=\mathrm{10}\sqrt{\mathrm{10}} \\ $$$$\left.{b}\right)\:{log}_{{x}} \mathrm{24}\:−\mathrm{3}{log}_{{x}} \mathrm{4}\:\:+\:\mathrm{2}{log}_{{x}} \mathrm{3}\:=−\mathrm{3} \\ $$$$\:\:\:\:\:\mathrm{log}_{\mathrm{x}} \mathrm{24}−\mathrm{log}_{\mathrm{x}} \mathrm{4}^{\mathrm{3}} +\mathrm{log}_{\mathrm{x}} \mathrm{3}^{\mathrm{2}} =−\mathrm{3} \\ $$$$\:\:\:\:\:\mathrm{log}_{\mathrm{x}} \left(\frac{\mathrm{24}×\mathrm{9}}{\mathrm{64}}\right)=−\mathrm{3} \\ $$$$\:\:\:\:\:\mathrm{log}_{\mathrm{x}} \left(\frac{\mathrm{27}}{\mathrm{8}}\right)=−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{−\mathrm{3}} =\frac{\mathrm{27}}{\mathrm{8}}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Rio Michael last updated on 15/Sep/19

$${thanks}\:{sir} \\ $$
