
Question Number 68609 by TawaTawa last updated on 14/Sep/19

Commented by TawaTawa last updated on 14/Sep/19
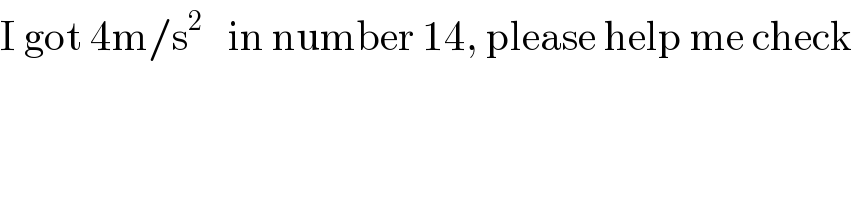
$$\mathrm{I}\:\mathrm{got}\:\mathrm{4m}/\mathrm{s}^{\mathrm{2}} \:\:\:\mathrm{in}\:\mathrm{number}\:\mathrm{14},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{check} \\ $$
Answered by mr W last updated on 14/Sep/19
![(13) s=t^3 −t^2 −t−2 v=(ds/dt)=3t^2 −2t−1 a=(dv/dt)=6t−2 a_(ave) =((∫_2 ^4 a(t)dt)/(4−2))=(([3t^2 −2t]_2 ^4 )/2)=((32)/2)=16 m/s^2 or a(4)=6×4−2=22 a(2)=6×2−2=10 a_(ave) =((22+10)/2)=16 m/s^2 (14) 3t^2 −2t−1=0 (3t+1)(t−1)=0 ⇒t=1 a(1)=6×1−2=4 m/s^2](Q68612.png)
$$\left(\mathrm{13}\right) \\ $$$${s}={t}^{\mathrm{3}} −{t}^{\mathrm{2}} −{t}−\mathrm{2} \\ $$$${v}=\frac{{ds}}{{dt}}=\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1} \\ $$$${a}=\frac{{dv}}{{dt}}=\mathrm{6}{t}−\mathrm{2} \\ $$$${a}_{{ave}} =\frac{\int_{\mathrm{2}} ^{\mathrm{4}} {a}\left({t}\right){dt}}{\mathrm{4}−\mathrm{2}}=\frac{\left[\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}\right]_{\mathrm{2}} ^{\mathrm{4}} }{\mathrm{2}}=\frac{\mathrm{32}}{\mathrm{2}}=\mathrm{16}\:{m}/{s}^{\mathrm{2}} \\ $$$${or} \\ $$$${a}\left(\mathrm{4}\right)=\mathrm{6}×\mathrm{4}−\mathrm{2}=\mathrm{22} \\ $$$${a}\left(\mathrm{2}\right)=\mathrm{6}×\mathrm{2}−\mathrm{2}=\mathrm{10} \\ $$$${a}_{{ave}} =\frac{\mathrm{22}+\mathrm{10}}{\mathrm{2}}=\mathrm{16}\:{m}/{s}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{14}\right) \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{3}{t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{1}\: \\ $$$${a}\left(\mathrm{1}\right)=\mathrm{6}×\mathrm{1}−\mathrm{2}=\mathrm{4}\:{m}/{s}^{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 14/Sep/19
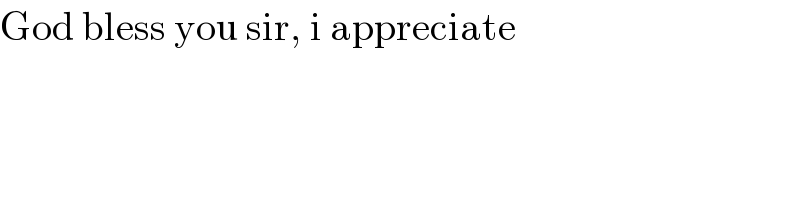
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$
