
Question Number 68598 by Abdo msup. last updated on 14/Sep/19
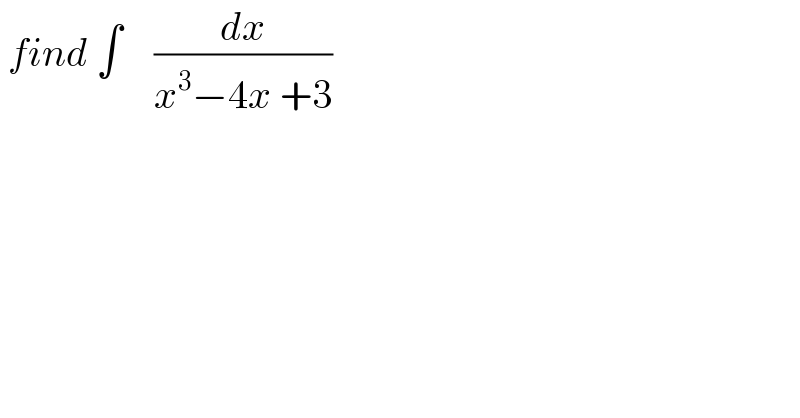
$$\:{find}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} −\mathrm{4}{x}\:+\mathrm{3}} \\ $$
Commented by turbo msup by abdo last updated on 14/Sep/19
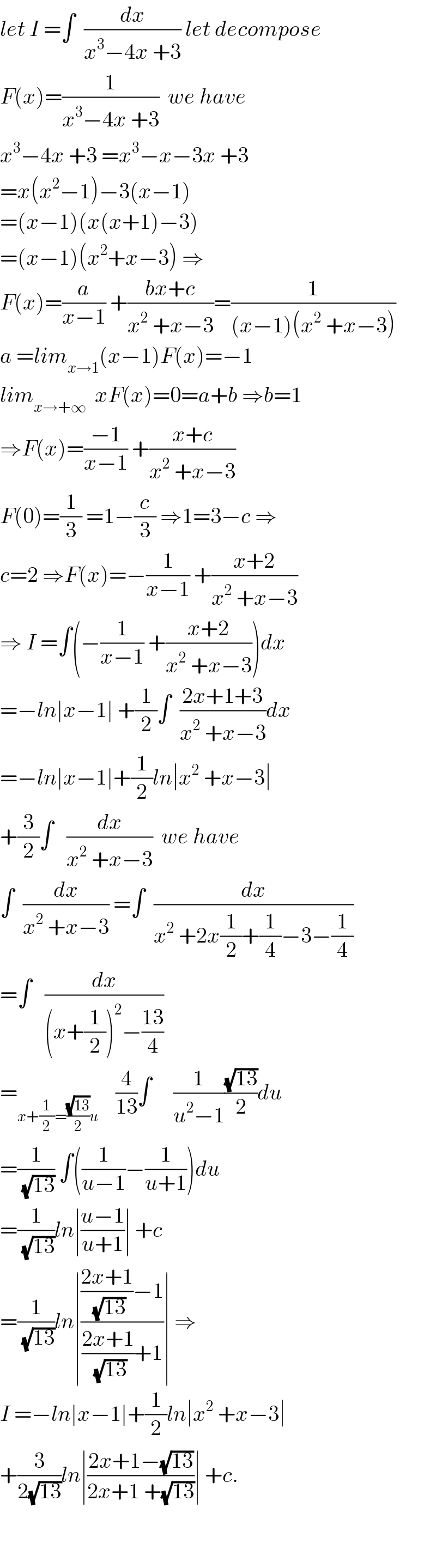
$${let}\:{I}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{3}} −\mathrm{4}{x}\:+\mathrm{3}}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{4}{x}\:+\mathrm{3}}\:\:{we}\:{have} \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}\:+\mathrm{3}\:={x}^{\mathrm{3}} −{x}−\mathrm{3}{x}\:+\mathrm{3} \\ $$$$={x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{3}\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}\left({x}+\mathrm{1}\right)−\mathrm{3}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}}=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}−\mathrm{3}\right)} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)=−\mathrm{1} \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:{xF}\left({x}\right)=\mathrm{0}={a}+{b}\:\Rightarrow{b}=\mathrm{1} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{−\mathrm{1}}{{x}−\mathrm{1}}\:+\frac{{x}+{c}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}} \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{3}}\:=\mathrm{1}−\frac{{c}}{\mathrm{3}}\:\Rightarrow\mathrm{1}=\mathrm{3}−{c}\:\Rightarrow \\ $$$${c}=\mathrm{2}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:+\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}} \\ $$$$\Rightarrow\:{I}\:=\int\left(−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:+\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}}\right){dx} \\ $$$$=−{ln}\mid{x}−\mathrm{1}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{3}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}}{dx} \\ $$$$=−{ln}\mid{x}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} \:+{x}−\mathrm{3}\mid \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}}\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{3}}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\int\:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{13}}{\mathrm{4}}} \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}{u}} \:\:\:\:\frac{\mathrm{4}}{\mathrm{13}}\int\:\:\:\:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{13}}}\:\int\left(\frac{\mathrm{1}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{13}}}{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\:+{c} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{13}}}{ln}\mid\frac{\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{13}}}−\mathrm{1}}{\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{13}}}+\mathrm{1}}\mid\:\Rightarrow \\ $$$${I}\:=−{ln}\mid{x}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} \:+{x}−\mathrm{3}\mid \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{13}}}{ln}\mid\frac{\mathrm{2}{x}+\mathrm{1}−\sqrt{\mathrm{13}}}{\mathrm{2}{x}+\mathrm{1}\:+\sqrt{\mathrm{13}}}\mid\:+{c}. \\ $$$$ \\ $$$$ \\ $$
Commented by som(math1967) last updated on 14/Sep/19

$$\int\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)} \\ $$$${let}\:\left({x}−\mathrm{1}\right)\left({Ax}+{B}\right)\:+{C}\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)=\mathrm{1} \\ $$$${putting}\:{x}=\mathrm{1}\:.....{C}=−\mathrm{1} \\ $$$${x}=\mathrm{0}\:........{B}=\mathrm{2} \\ $$$${x}=−\mathrm{1}........{A}=\mathrm{1} \\ $$$$\therefore\int\frac{\left\{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)−\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)\right\}{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)}\: \\ $$$$=\int\frac{\left({x}+\mathrm{2}\right){dx}}{\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)}\:−\int\frac{{dx}}{\left({x}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{2}{x}+\mathrm{4}\right){dx}}{{x}^{\mathrm{2}} +{x}−\mathrm{3}}\:−{ln}\left({x}−\mathrm{1}\right)\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)}{\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)}\:+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:−{lnx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)\:+\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\sqrt{\mathrm{13}}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}}\right)−{ln}\left({x}−\mathrm{1}\right)+{K} \\ $$
