
Question Number 68595 by Abdo msup. last updated on 14/Sep/19
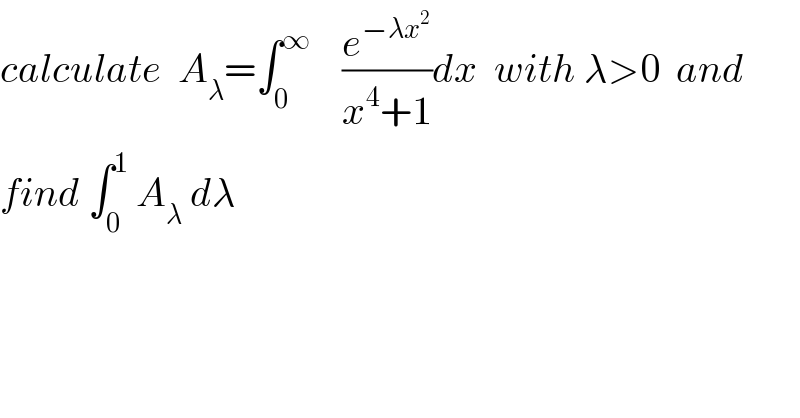
$${calculate}\:\:{A}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} +\mathrm{1}}{dx}\:\:{with}\:\lambda>\mathrm{0}\:\:{and}\: \\ $$ $${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{A}_{\lambda} \:{d}\lambda \\ $$
Commented bymathmax by abdo last updated on 14/Sep/19
![A_λ = ∫_0 ^∞ (e^(−λx^2 ) /(x^4 +1))dx ⇒2A_λ =∫_(−∞) ^(+∞) (e^(−λx^2 ) /(x^4 +1))dx let W(z) =(e^(−λz^2 ) /(z^4 +1)) poles of W? we have W(z) =(e^(−λx^2 ) /((z^2 −i)(z^2 +i))) =(e^(−λx^2 ) /((z−(√i))(z+(√i))(z−(√(−i)))(2+(√(−i))))) =(e^(−λx^2 ) /((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) so the poles of W are +^− e^((iπ)/4) and +^− e^(−((iπ)/4)) residus tbeorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ{Res(W,e^((iπ)/4) )+Res(W,−e^(−((iπ)/4)) )} Res(W,e^((iπ)/4) ) =(e^(−λ(i)) /(2e^((iπ)/4) (2i))) =(1/(4i)) e^(−λi−((iπ)/4)) =(1/(4i))e^(−(λ+(π/4))i) Res(W,−e^(−((iπ)/4)) ) = (e^(−λ(−i)) /((−2i)(−2e^(−((iπ)/4)) ))) =(1/(4i)) e^(λi+((iπ)/4)) =(1/(4i)) e^((λ+(π/4))i) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ{ (1/(4i))e^(−(λ+(π/4))i) +(1/(4i)) e^((λ+(π/4))i) } =(π/2){ 2Re(e^((λ+(π/4))i) ) =π cos((π/4) +λ) ⇒A_λ =(π/2)cos((π/4) +λ) ∫_0 ^1 A_λ dλ =(π/2) ∫_0 ^1 cos(λ+(π/4)) =[sin(λ+(π/4))]_0 ^1 =sin(1+(π/4))−((√2)/2)](Q68687.png)
$${A}_{\lambda} =\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} \:+\mathrm{1}}{dx}\:\Rightarrow\mathrm{2}{A}_{\lambda} =\int_{−\infty} ^{+\infty} \:\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} \:+\mathrm{1}}{dx}\:{let}\:{W}\left({z}\right)\:=\frac{{e}^{−\lambda{z}^{\mathrm{2}} } }{{z}^{\mathrm{4}} +\mathrm{1}} \\ $$ $${poles}\:{of}\:{W}?\:\:{we}\:{have}\:{W}\left({z}\right)\:=\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} +{i}\right)} \\ $$ $$=\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{\left({z}−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)\left({z}−\sqrt{−{i}}\right)\left(\mathrm{2}+\sqrt{−{i}}\right)}\:=\frac{{e}^{−\lambda{x}^{\mathrm{2}} } }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$ $${so}\:{the}\:{poles}\:{of}\:{W}\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{and}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$ $${residus}\:{tbeorem}\:{give}\: \\ $$ $$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{{Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$ $${Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{{e}^{−\lambda\left({i}\right)} }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{−\lambda{i}−\frac{{i}\pi}{\mathrm{4}}} \:=\frac{\mathrm{1}}{\mathrm{4}{i}}{e}^{−\left(\lambda+\frac{\pi}{\mathrm{4}}\right){i}} \\ $$ $${Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\:\frac{{e}^{−\lambda\left(−{i}\right)} }{\left(−\mathrm{2}{i}\right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{\lambda{i}+\frac{{i}\pi}{\mathrm{4}}} =\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{\left(\lambda+\frac{\pi}{\mathrm{4}}\right){i}} \:\Rightarrow \\ $$ $$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{4}{i}}{e}^{−\left(\lambda+\frac{\pi}{\mathrm{4}}\right){i}} \:+\frac{\mathrm{1}}{\mathrm{4}{i}}\:{e}^{\left(\lambda+\frac{\pi}{\mathrm{4}}\right){i}} \right\} \\ $$ $$=\frac{\pi}{\mathrm{2}}\left\{\:\mathrm{2}{Re}\left({e}^{\left(\lambda+\frac{\pi}{\mathrm{4}}\right){i}} \right)\:=\pi\:\:{cos}\left(\frac{\pi}{\mathrm{4}}\:+\lambda\right)\:\Rightarrow{A}_{\lambda} =\frac{\pi}{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}\:+\lambda\right)\right. \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:{A}_{\lambda} {d}\lambda\:=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{cos}\left(\lambda+\frac{\pi}{\mathrm{4}}\right)\:=\left[{sin}\left(\lambda+\frac{\pi}{\mathrm{4}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:={sin}\left(\mathrm{1}+\frac{\pi}{\mathrm{4}}\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
