
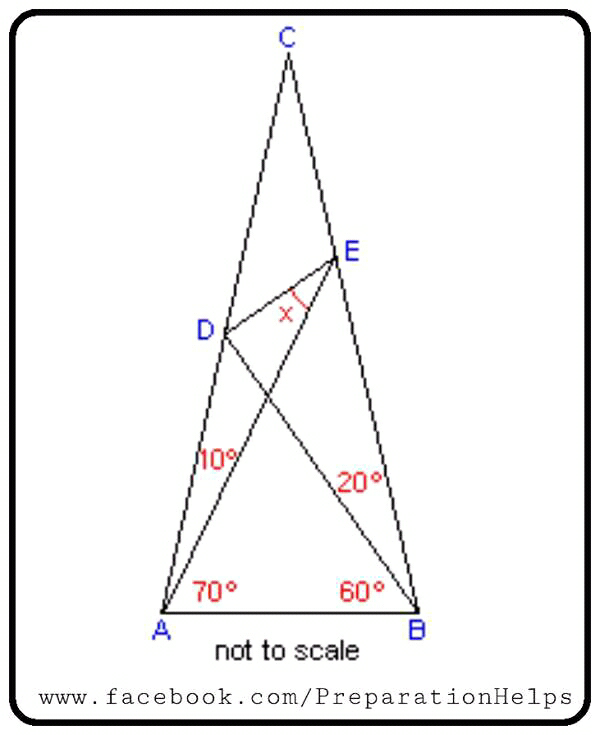
Question Number 6852 by Tawakalitu. last updated on 31/Jul/16
Commented by Tawakalitu. last updated on 31/Jul/16
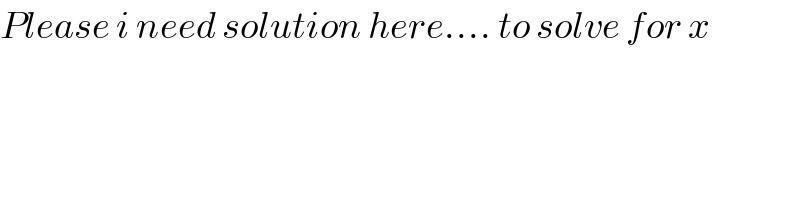
$${Please}\:{i}\:{need}\:{solution}\:{here}....\:{to}\:{solve}\:{for}\:{x} \\ $$
Answered by Rasheed Soomro last updated on 03/Aug/16
Commented by Rasheed Soomro last updated on 05/Aug/16

$${By}\:{GeoGebra}\:\:\:{x}=\mathrm{20}° \\ $$$${With}\:{given}\:{angles}\:{x}\:{can}'{t}\:{be} \\ $$$${determined}. \\ $$$${I}\:{think}\:{one}\:{should}\:{consider} \\ $$$${measures}\:{of}\:{the}\:{sides}\:{in}\:{order} \\ $$$${to}\:{determine}\:{the}\:{required}\:{angle}. \\ $$
Answered by Rasheed Soomro last updated on 07/Aug/16
![For diagram see comment below. In △ACB ∠CAB=10+70=80 and ∠CBA=20+60=80 ∵ ∠CAB=∠CBA=80 ∴ AC=BC [Opposite sides to congruent angles] Also ∠C=180−2×80=20 In △AFB, ∠AFB=180−70−60=50 So, ∠EFB=180−50=130 and in △EFB ∠FEB=180−20−130=30 Let AC=BC=1 In △AEC , AC=1,∠C=20,∠CAE=10 So, ∠AEC=180−20−10=150 By Sine law ((CE)/(sin 10))=((AC)/(sin 150))=(1/(sin 150)) CE=((sin 10)/(sin 150)) Similarly in △BDC, BC=1,∠C=20,∠CBD=20 & ∠BDC=140 ((CD)/(sin 20))=((BC)/(sin 140))=(1/(sin 140)) CD=((sin 20)/(sin 140)) Now in △CDE, According to Sine law ((CE)/(sin (160−y)))=((CD)/(sin y)) ((sin (160−y))/(sin y))=((CE)/(CD))=((sin 10)/(sin 150))/((sin 20)/(sin 140)) ((sin 160 cos y−cos 160 sin y)/(sin y))=((sin 10 sin 140)/(sin 20sin 150)) sin 160 cot y=((sin 10 sin 140)/(sin 20sin 150))+cos 160 =((sin 10 sin 140+sin 20sin 150cos 160)/(sin 20sin 150)) cot y=((sin 10 sin 140+sin 20sin 150cos 160)/(sin 20sin 150sin 160)) tan y=((sin 20sin 150sin 160)/(sin 10 sin 140+sin 20 sin 150 cos 160)) y=tan^(−1) (((sin 20sin 150sin 160)/(sin 10 sin 140+sin 20 sin 150 cos 160)))=130 (If 0<y<180) [With the help of calculator] x=180−y−30=150−130=20](Q7007.png)
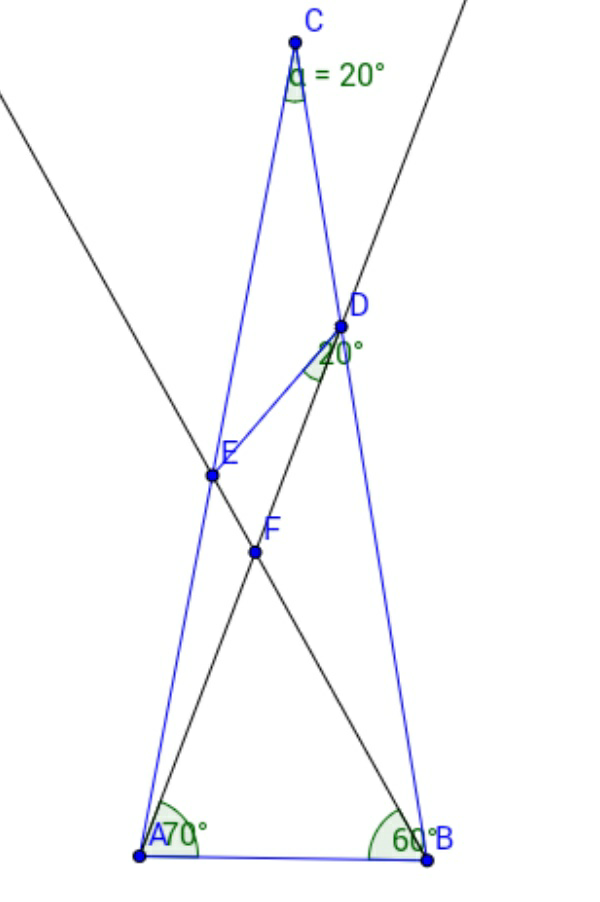
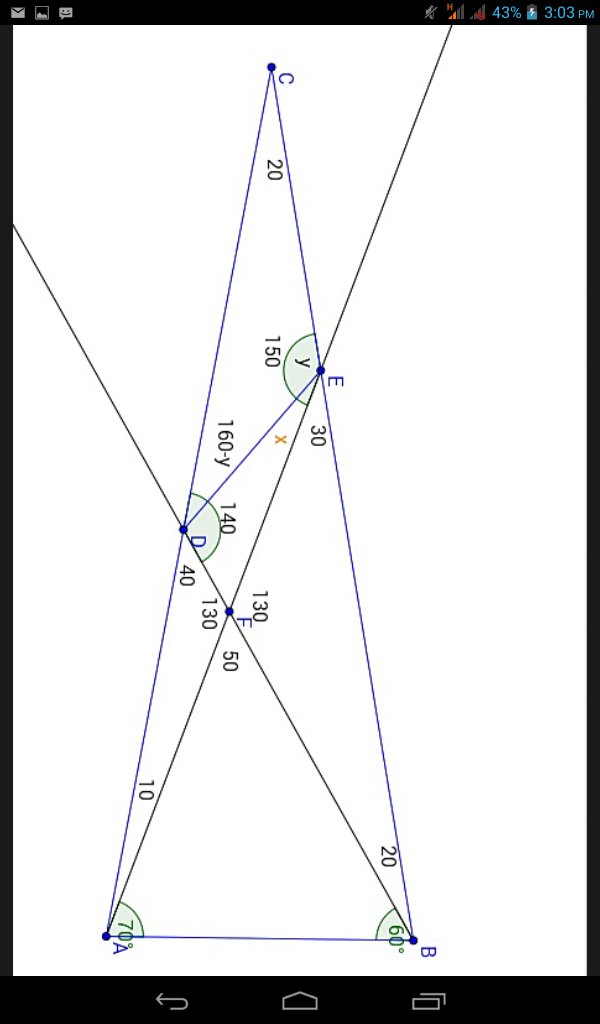
$${For}\:{diagram}\:{see}\:{comment}\:{below}. \\ $$$${In}\:\bigtriangleup{ACB}\:\:\:\:\: \\ $$$$\:\:\:\:\angle{CAB}=\mathrm{10}+\mathrm{70}=\mathrm{80}\:\:{and}\:\:\:\angle{CBA}=\mathrm{20}+\mathrm{60}=\mathrm{80} \\ $$$$\because\:\:\:\angle{CAB}=\angle{CBA}=\mathrm{80} \\ $$$$\therefore\:{AC}={BC}\:\:\:\left[{Opposite}\:{sides}\:{to}\:{congruent}\:{angles}\right] \\ $$$${Also}\:\:\angle{C}=\mathrm{180}−\mathrm{2}×\mathrm{80}=\mathrm{20} \\ $$$${In}\:\bigtriangleup{AFB},\:\:\:\:\angle{AFB}=\mathrm{180}−\mathrm{70}−\mathrm{60}=\mathrm{50} \\ $$$${So},\:\:\:\:\angle{EFB}=\mathrm{180}−\mathrm{50}=\mathrm{130} \\ $$$${and}\:{in}\:\bigtriangleup{EFB}\:\:\:\:\:\:\angle{FEB}=\mathrm{180}−\mathrm{20}−\mathrm{130}=\mathrm{30} \\ $$$$ \\ $$$${Let}\:\:{AC}={BC}=\mathrm{1} \\ $$$${In}\:\bigtriangleup{AEC}\:,\:\:\:\:\:{AC}=\mathrm{1},\angle{C}=\mathrm{20},\angle{CAE}=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{So},\:\:\:\:\:\:\:\:\:\:\angle{AEC}=\mathrm{180}−\mathrm{20}−\mathrm{10}=\mathrm{150} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{By}\:{Sine}\:{law} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CE}}{\mathrm{sin}\:\mathrm{10}}=\frac{{AC}}{\mathrm{sin}\:\mathrm{150}}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{150}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{CE}=\frac{\mathrm{sin}\:\mathrm{10}}{\mathrm{sin}\:\mathrm{150}} \\ $$$$\:{Similarly}\:{in}\:\bigtriangleup{BDC},\:\:\:{BC}=\mathrm{1},\angle{C}=\mathrm{20},\angle{CBD}=\mathrm{20}\:\&\:\angle{BDC}=\mathrm{140} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CD}}{\mathrm{sin}\:\mathrm{20}}=\frac{{BC}}{\mathrm{sin}\:\mathrm{140}}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{140}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{CD}=\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{140}} \\ $$$$ \\ $$$${Now}\:{in}\:\bigtriangleup{CDE},\:\:\:{According}\:{to}\:{Sine}\:{law} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CE}}{\mathrm{sin}\:\left(\mathrm{160}−{y}\right)}=\frac{{CD}}{\mathrm{sin}\:{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{sin}\:\left(\mathrm{160}−{y}\right)}{\mathrm{sin}\:{y}}=\frac{{CE}}{{CD}}=\frac{\mathrm{sin}\:\mathrm{10}}{\mathrm{sin}\:\mathrm{150}}/\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{140}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{160}\:\mathrm{cos}\:{y}−\mathrm{cos}\:\mathrm{160}\:\mathrm{sin}\:{y}}{\mathrm{sin}\:{y}}=\frac{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}}{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{160}\:\mathrm{cot}\:{y}=\frac{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}}{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150}}+\mathrm{cos}\:\mathrm{160} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}+\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150cos}\:\mathrm{160}}{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cot}\:{y}=\frac{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}+\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150cos}\:\mathrm{160}}{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150sin}\:\mathrm{160}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{tan}\:{y}=\frac{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150sin}\:\mathrm{160}}{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}+\mathrm{sin}\:\mathrm{20}\:\mathrm{sin}\:\mathrm{150}\:\mathrm{cos}\:\mathrm{160}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{20sin}\:\mathrm{150sin}\:\mathrm{160}}{\mathrm{sin}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{140}+\mathrm{sin}\:\mathrm{20}\:\mathrm{sin}\:\mathrm{150}\:\mathrm{cos}\:\mathrm{160}}\right)=\mathrm{130}\:\left({If}\:\mathrm{0}<{y}<\mathrm{180}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{With}\:{the}\:{help}\:{of}\:\:{calculator}\right] \\ $$$$\:\:\:\:\:\:\:{x}=\mathrm{180}−{y}−\mathrm{30}=\mathrm{150}−\mathrm{130}=\mathrm{20} \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 05/Aug/16
Commented by Tawakalitu. last updated on 20/Aug/16
$${Wow},\:{thanks}\:{so}\:{much}.\:{i}\:{did}\:{not}\:{see}\:{it}\:{before}.\:{I}\:{really}\:{appreciate} \\ $$$$.\:{Thanks}\:{again}. \\ $$
