
Question Number 68495 by Maclaurin Stickker last updated on 12/Sep/19
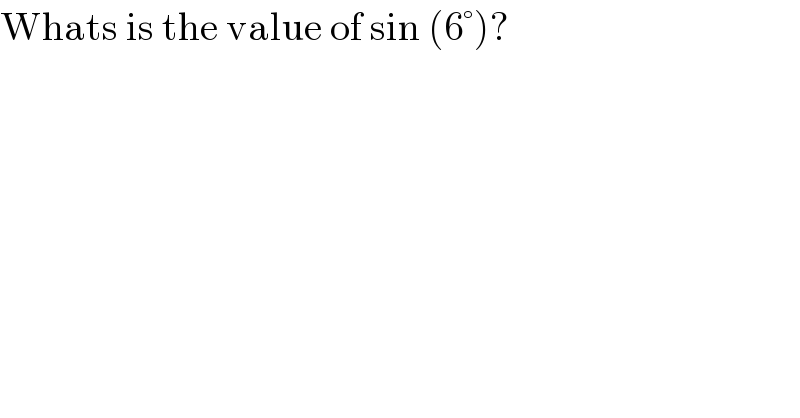
$$\mathrm{Whats}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\left(\mathrm{6}°\right)? \\ $$
Commented by Pk1167156@gmail.com last updated on 12/Sep/19

$$\mathrm{soln} \\ $$$$\mathrm{sin6}° \\ $$$$=\mathrm{sin}\left(\mathrm{36}−\mathrm{30}\right) \\ $$$$=\mathrm{sin36}°\mathrm{cos30}°−\mathrm{cos36}°\mathrm{sin30}° \\ $$$$=\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{30}−\mathrm{6}\sqrt{\mathrm{5}}}}{\mathrm{8}}−\frac{\sqrt{\mathrm{5}+\mathrm{1}}}{\mathrm{8}} \\ $$$$=\frac{\sqrt{\mathrm{30}−\mathrm{6}\sqrt{\mathrm{5}}}−\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{8}} \\ $$
Answered by MJS last updated on 12/Sep/19
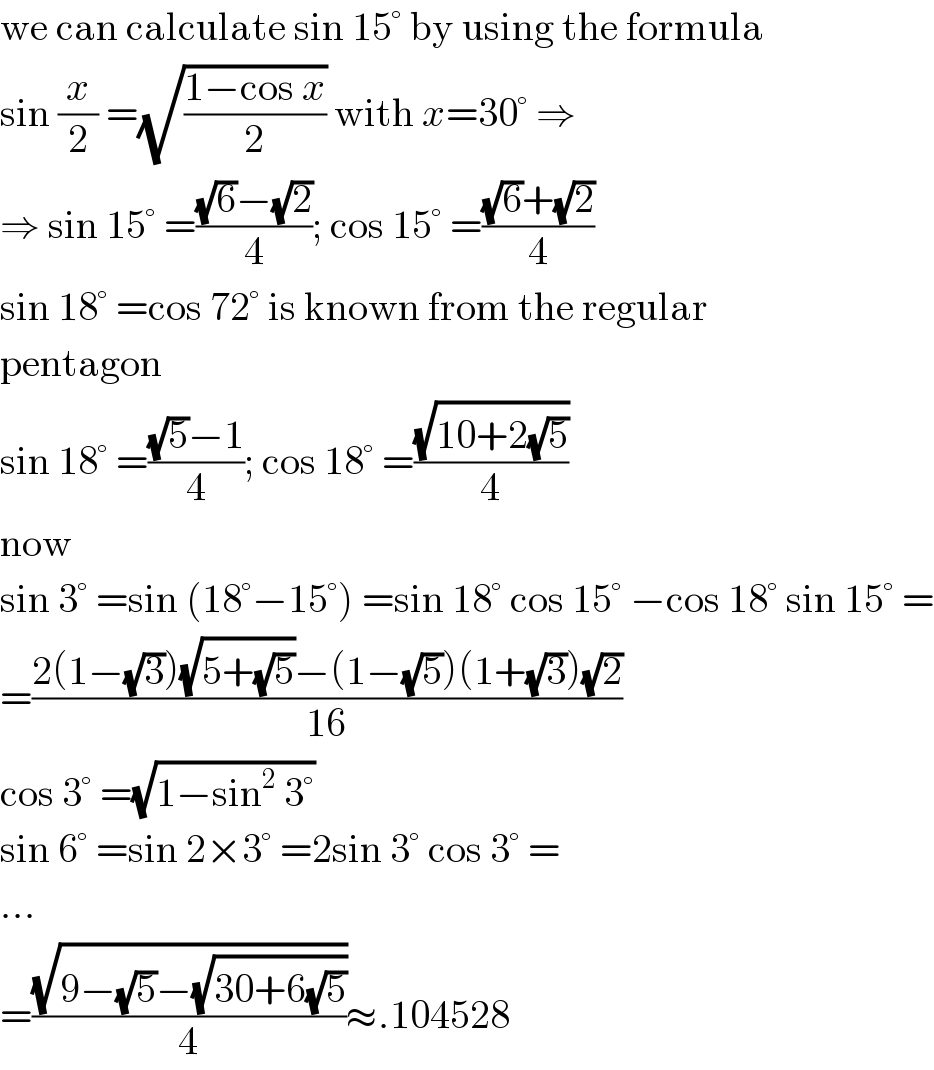
$$\mathrm{we}\:\mathrm{can}\:\mathrm{calculate}\:\mathrm{sin}\:\mathrm{15}°\:\mathrm{by}\:\mathrm{using}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\:=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{2}}}\:\mathrm{with}\:{x}=\mathrm{30}°\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{15}°\:=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}};\:\mathrm{cos}\:\mathrm{15}°\:=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{18}°\:=\mathrm{cos}\:\mathrm{72}°\:\mathrm{is}\:\mathrm{known}\:\mathrm{from}\:\mathrm{the}\:\mathrm{regular} \\ $$$$\mathrm{pentagon} \\ $$$$\mathrm{sin}\:\mathrm{18}°\:=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}};\:\mathrm{cos}\:\mathrm{18}°\:=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$$\mathrm{now} \\ $$$$\mathrm{sin}\:\mathrm{3}°\:=\mathrm{sin}\:\left(\mathrm{18}°−\mathrm{15}°\right)\:=\mathrm{sin}\:\mathrm{18}°\:\mathrm{cos}\:\mathrm{15}°\:−\mathrm{cos}\:\mathrm{18}°\:\mathrm{sin}\:\mathrm{15}°\:= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}−\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$$\mathrm{cos}\:\mathrm{3}°\:=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\mathrm{3}°} \\ $$$$\mathrm{sin}\:\mathrm{6}°\:=\mathrm{sin}\:\mathrm{2}×\mathrm{3}°\:=\mathrm{2sin}\:\mathrm{3}°\:\mathrm{cos}\:\mathrm{3}°\:= \\ $$$$... \\ $$$$=\frac{\sqrt{\mathrm{9}−\sqrt{\mathrm{5}}−\sqrt{\mathrm{30}+\mathrm{6}\sqrt{\mathrm{5}}}}}{\mathrm{4}}\approx.\mathrm{104528} \\ $$
Commented by MJS last updated on 12/Sep/19
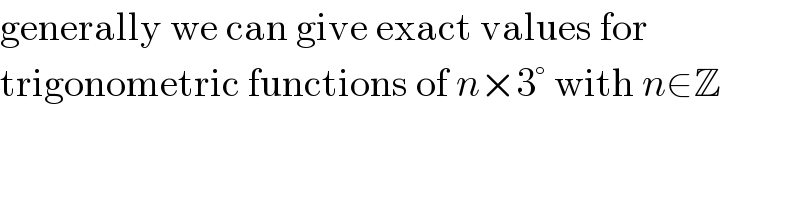
$$\mathrm{generally}\:\mathrm{we}\:\mathrm{can}\:\mathrm{give}\:\mathrm{exact}\:\mathrm{values}\:\mathrm{for} \\ $$$$\mathrm{trigonometric}\:\mathrm{functions}\:\mathrm{of}\:{n}×\mathrm{3}°\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$
Commented by Maclaurin Stickker last updated on 12/Sep/19

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{sir}! \\ $$
Commented by malwaan last updated on 13/Sep/19

$$\boldsymbol{{great}}\:\boldsymbol{{work}} \\ $$$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\heartsuit \\ $$
Commented by Maclaurin Stickker last updated on 12/Sep/19
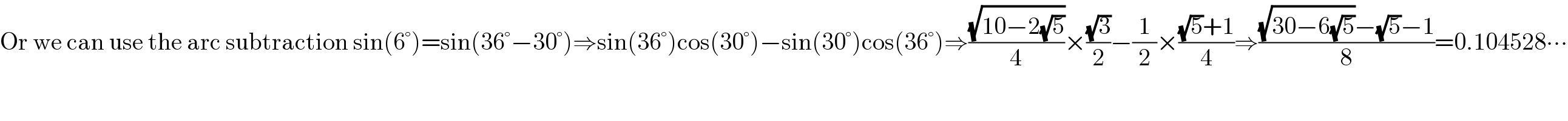
$$\mathrm{Or}\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{subtraction}\:\mathrm{sin}\left(\mathrm{6}°\right)=\mathrm{sin}\left(\mathrm{36}°−\mathrm{30}°\right)\Rightarrow\mathrm{sin}\left(\mathrm{36}°\right)\mathrm{cos}\left(\mathrm{30}°\right)−\mathrm{sin}\left(\mathrm{30}°\right)\mathrm{cos}\left(\mathrm{36}°\right)\Rightarrow\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\Rightarrow\frac{\sqrt{\mathrm{30}−\mathrm{6}\sqrt{\mathrm{5}}}−\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{8}}=\mathrm{0}.\mathrm{104528}\centerdot\centerdot\centerdot \\ $$
