
Question Number 68481 by ajfour last updated on 11/Sep/19
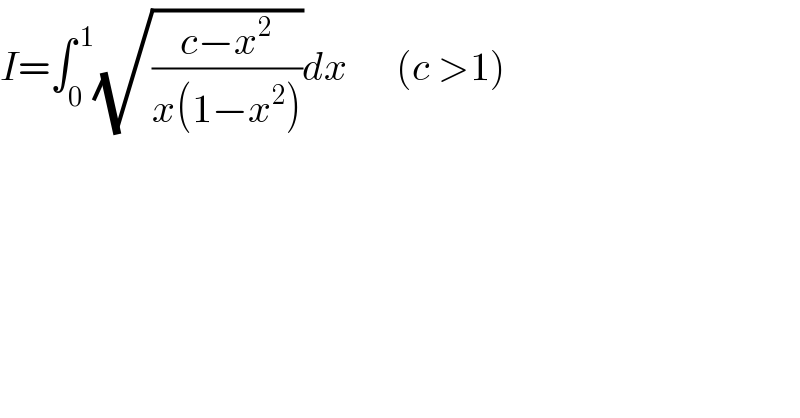
$${I}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\frac{{c}−{x}^{\mathrm{2}} }{{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}}{dx}\:\:\:\:\:\:\left({c}\:>\mathrm{1}\right) \\ $$
Commented byMJS last updated on 11/Sep/19
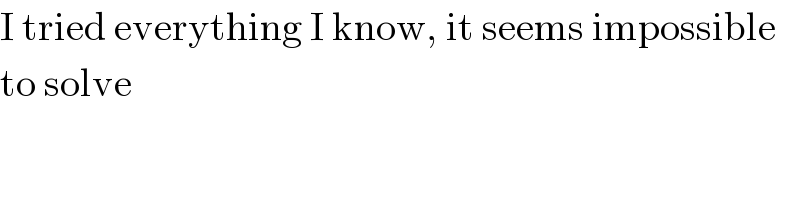
$$\mathrm{I}\:\mathrm{tried}\:\mathrm{everything}\:\mathrm{I}\:\mathrm{know},\:\mathrm{it}\:\mathrm{seems}\:\mathrm{impossible} \\ $$ $$\mathrm{to}\:\mathrm{solve} \\ $$
Commented byKunal12588 last updated on 12/Sep/19

Commented byKunal12588 last updated on 12/Sep/19

Commented byMJS last updated on 12/Sep/19
![((2x(√(1−x^2 ))(√((c−x^2 )/(x−x^3 ))))/(√(1−(x^2 /c))))=2(√(cx)) ⇒ [2(√(cx))F_1 (...)]_0 ^1 =2(√c)F_1 ((1/4); −(1/2), (1/2); (5/4); (1/c), 1)](Q68505.png)
$$\frac{\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\sqrt{\frac{{c}−{x}^{\mathrm{2}} }{{x}−{x}^{\mathrm{3}} }}}{\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{c}}}}=\mathrm{2}\sqrt{{cx}} \\ $$ $$\Rightarrow\:\left[\mathrm{2}\sqrt{{cx}}\mathrm{F}_{\mathrm{1}} \left(...\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}\sqrt{{c}}\mathrm{F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}};\:−\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\mathrm{5}}{\mathrm{4}};\:\frac{\mathrm{1}}{{c}},\:\mathrm{1}\right) \\ $$
Commented byMJS last updated on 12/Sep/19
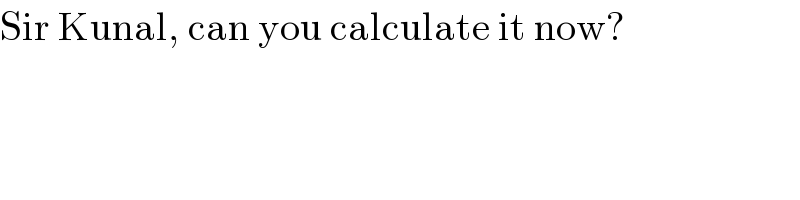
$$\mathrm{Sir}\:\mathrm{Kunal},\:\mathrm{can}\:\mathrm{you}\:\mathrm{calculate}\:\mathrm{it}\:\mathrm{now}? \\ $$
Commented byMJS last updated on 12/Sep/19
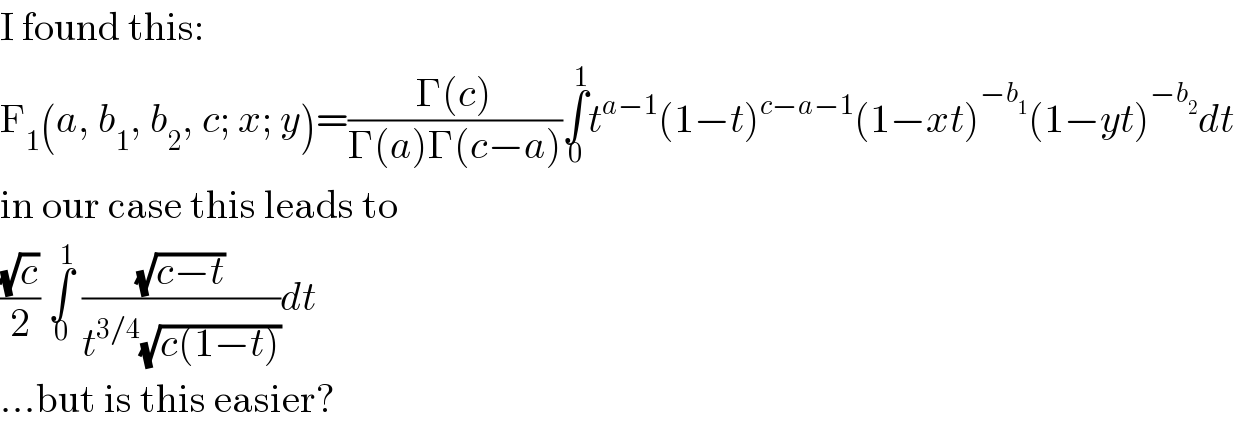
$$\mathrm{I}\:\mathrm{found}\:\mathrm{this}: \\ $$ $$\mathrm{F}_{\mathrm{1}} \left({a},\:{b}_{\mathrm{1}} ,\:{b}_{\mathrm{2}} ,\:{c};\:{x};\:{y}\right)=\frac{\Gamma\left({c}\right)}{\Gamma\left({a}\right)\Gamma\left({c}−{a}\right)}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{c}−{a}−\mathrm{1}} \left(\mathrm{1}−{xt}\right)^{−{b}_{\mathrm{1}} } \left(\mathrm{1}−{yt}\right)^{−{b}_{\mathrm{2}} } {dt} \\ $$ $$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$ $$\frac{\sqrt{{c}}}{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\sqrt{{c}−{t}}}{{t}^{\mathrm{3}/\mathrm{4}} \sqrt{{c}\left(\mathrm{1}−{t}\right)}}{dt} \\ $$ $$...\mathrm{but}\:\mathrm{is}\:\mathrm{this}\:\mathrm{easier}? \\ $$
