
Question Number 68446 by 9102176137086 last updated on 10/Sep/19
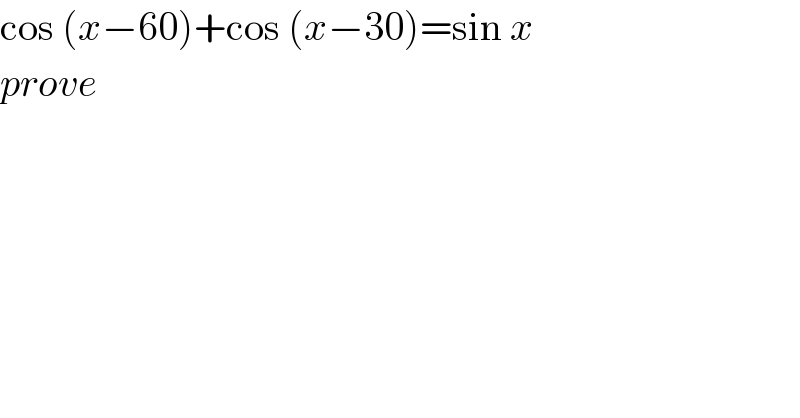
$$\mathrm{cos}\:\left({x}−\mathrm{60}\right)+\mathrm{cos}\:\left({x}−\mathrm{30}\right)=\mathrm{sin}\:{x} \\ $$$${prove} \\ $$
Commented by mr W last updated on 10/Sep/19
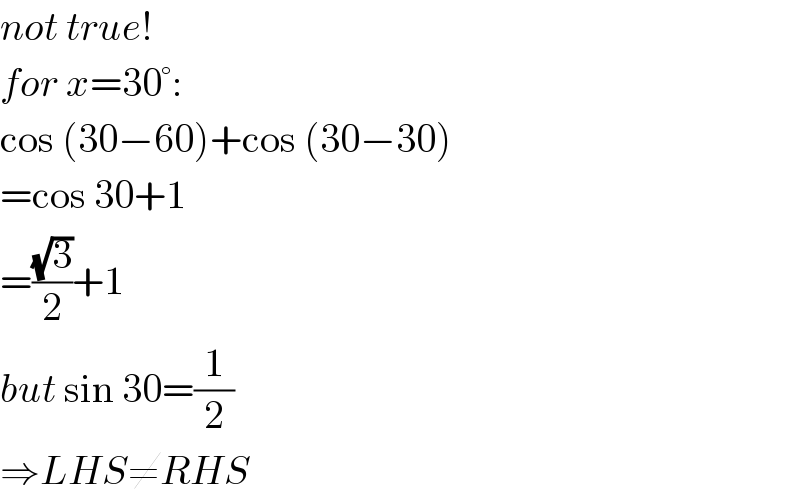
$${not}\:{true}! \\ $$$${for}\:{x}=\mathrm{30}°: \\ $$$$\mathrm{cos}\:\left(\mathrm{30}−\mathrm{60}\right)+\mathrm{cos}\:\left(\mathrm{30}−\mathrm{30}\right) \\ $$$$=\mathrm{cos}\:\mathrm{30}+\mathrm{1} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1} \\ $$$${but}\:\mathrm{sin}\:\mathrm{30}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{LHS}\neq{RHS} \\ $$
