
Question Number 68418 by necxxx last updated on 10/Sep/19

Commented by necxxx last updated on 10/Sep/19

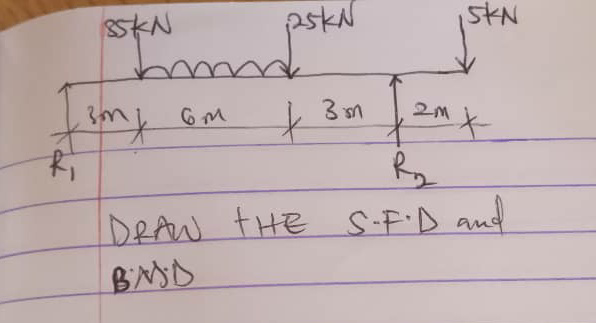
$${The}\:{UDL}\:{is}\:\mathrm{2}.\mathrm{5}{KN}/{m}.\:{The}\:{first}\:{point} \\ $$$${load}\:{is}\:\mathrm{35}{KN}.\:{I}'{ve}\:{tried}\:{solving}\:{but}\:{I} \\ $$$${encountered}\:{some}\:{issues}\:{with}\:{the}\:{diagram}. \\ $$$${I}'{ll}\:{be}\:{really}\:{grateful}\:{to}\:{get}\:{this}\:{solved} \\ $$$${with}\:{the}\:{possible}\:{diagrams}. \\ $$
Commented by mr W last updated on 10/Sep/19
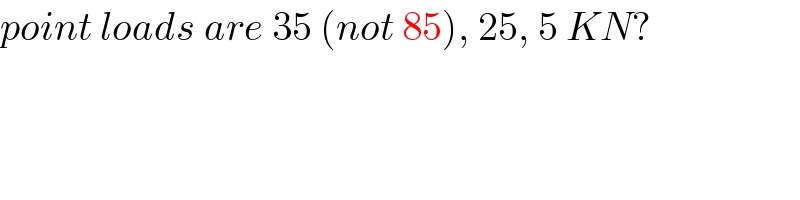
$${point}\:{loads}\:{are}\:\mathrm{35}\:\left({not}\:\mathrm{85}\right),\:\mathrm{25},\:\mathrm{5}\:{KN}? \\ $$
Commented by necxxx last updated on 10/Sep/19
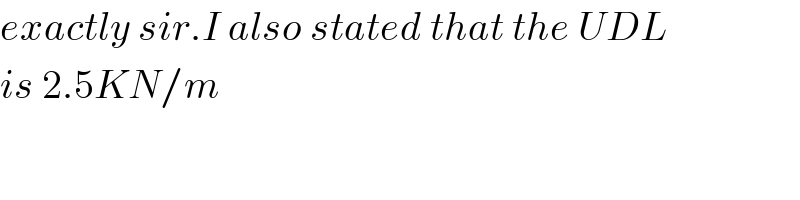
$${exactly}\:{sir}.{I}\:{also}\:{stated}\:{that}\:{the}\:{UDL} \\ $$$${is}\:\mathrm{2}.\mathrm{5}{KN}/{m} \\ $$
Answered by mr W last updated on 10/Sep/19
Commented by mr W last updated on 10/Sep/19
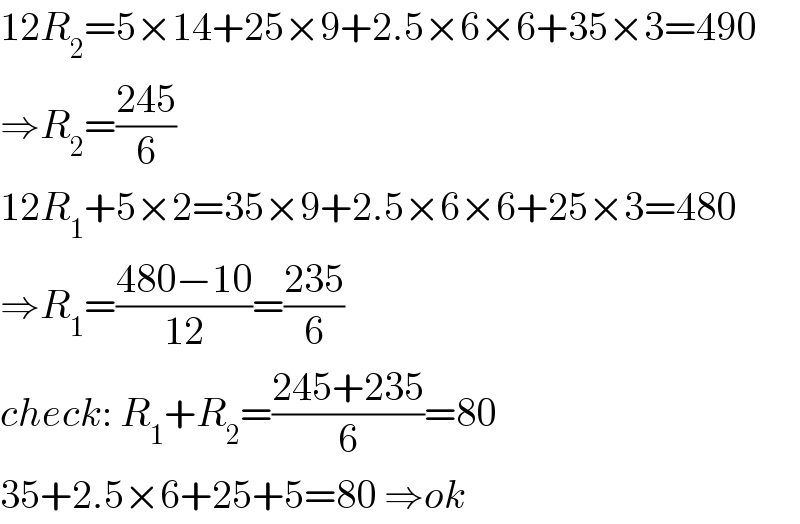
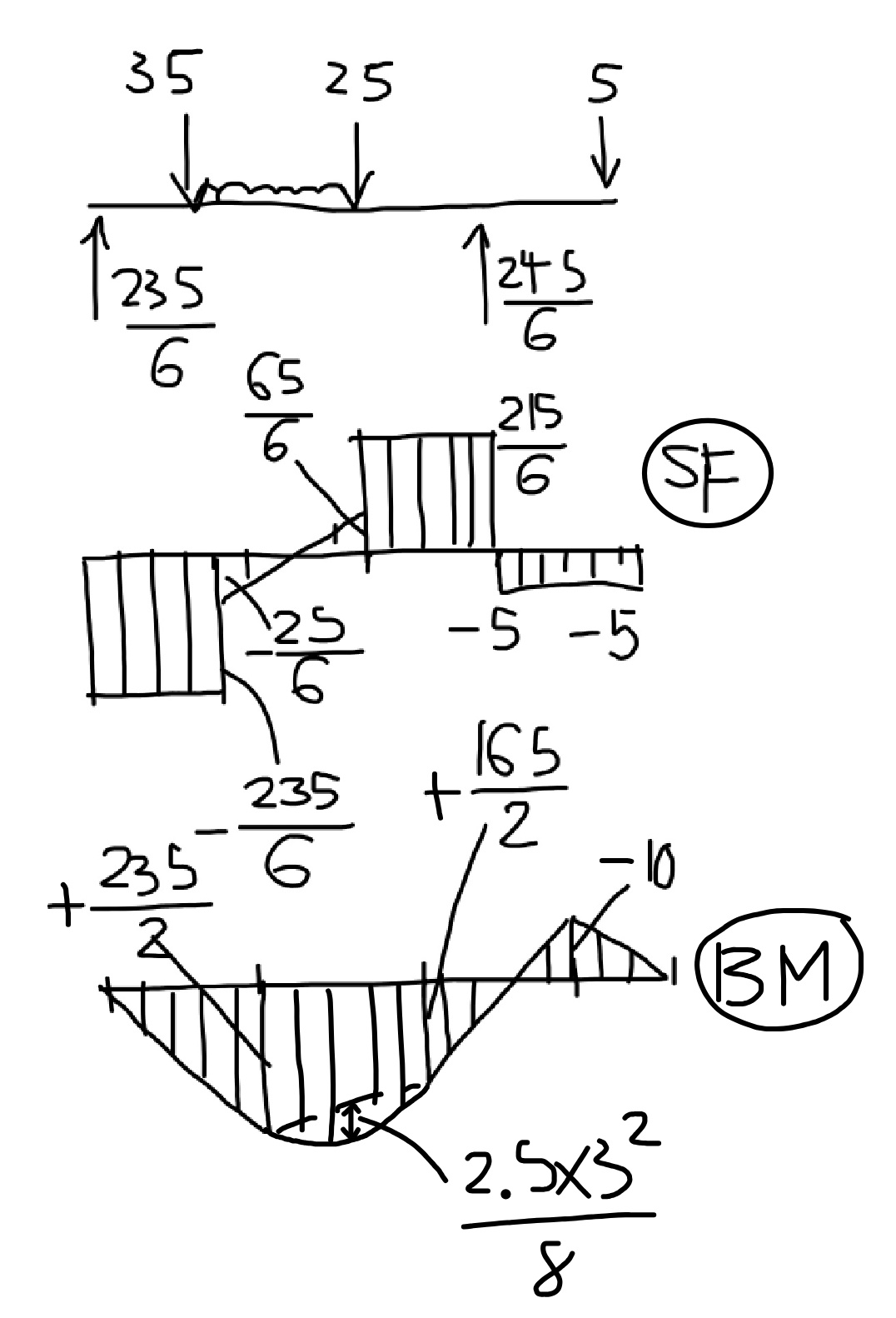
$$\mathrm{12}{R}_{\mathrm{2}} =\mathrm{5}×\mathrm{14}+\mathrm{25}×\mathrm{9}+\mathrm{2}.\mathrm{5}×\mathrm{6}×\mathrm{6}+\mathrm{35}×\mathrm{3}=\mathrm{490} \\ $$$$\Rightarrow{R}_{\mathrm{2}} =\frac{\mathrm{245}}{\mathrm{6}} \\ $$$$\mathrm{12}{R}_{\mathrm{1}} +\mathrm{5}×\mathrm{2}=\mathrm{35}×\mathrm{9}+\mathrm{2}.\mathrm{5}×\mathrm{6}×\mathrm{6}+\mathrm{25}×\mathrm{3}=\mathrm{480} \\ $$$$\Rightarrow{R}_{\mathrm{1}} =\frac{\mathrm{480}−\mathrm{10}}{\mathrm{12}}=\frac{\mathrm{235}}{\mathrm{6}} \\ $$$${check}:\:{R}_{\mathrm{1}} +{R}_{\mathrm{2}} =\frac{\mathrm{245}+\mathrm{235}}{\mathrm{6}}=\mathrm{80} \\ $$$$\mathrm{35}+\mathrm{2}.\mathrm{5}×\mathrm{6}+\mathrm{25}+\mathrm{5}=\mathrm{80}\:\Rightarrow{ok} \\ $$
Commented by mr W last updated on 10/Sep/19
Commented by mr W last updated on 10/Sep/19
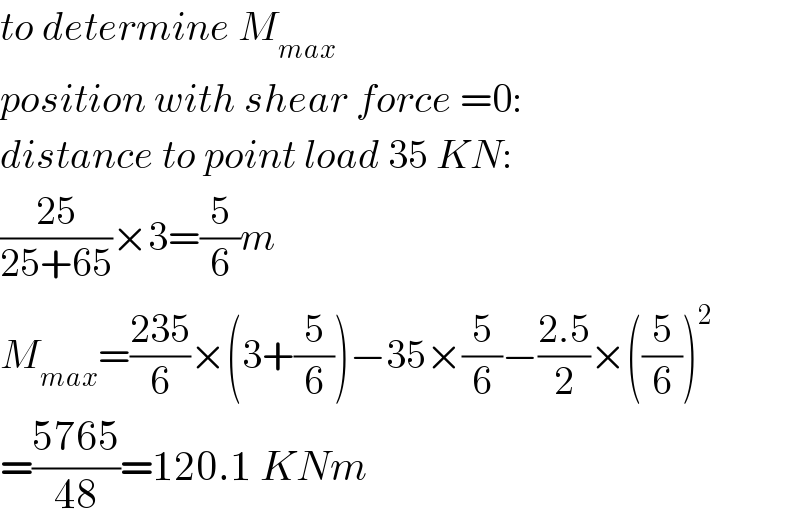
$${to}\:{determine}\:{M}_{{max}} \\ $$$${position}\:{with}\:{shear}\:{force}\:=\mathrm{0}: \\ $$$${distance}\:{to}\:{point}\:{load}\:\mathrm{35}\:{KN}: \\ $$$$\frac{\mathrm{25}}{\mathrm{25}+\mathrm{65}}×\mathrm{3}=\frac{\mathrm{5}}{\mathrm{6}}{m} \\ $$$${M}_{{max}} =\frac{\mathrm{235}}{\mathrm{6}}×\left(\mathrm{3}+\frac{\mathrm{5}}{\mathrm{6}}\right)−\mathrm{35}×\frac{\mathrm{5}}{\mathrm{6}}−\frac{\mathrm{2}.\mathrm{5}}{\mathrm{2}}×\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{5765}}{\mathrm{48}}=\mathrm{120}.\mathrm{1}\:{KNm} \\ $$
Commented by necxxx last updated on 10/Sep/19
$${Thank}\:{you}\:{so}\:{much}\:{mrW}.{I}'{m}\:{very}\:{grateful} \\ $$
