
Question Number 6834 by nburiburu last updated on 30/Jul/16
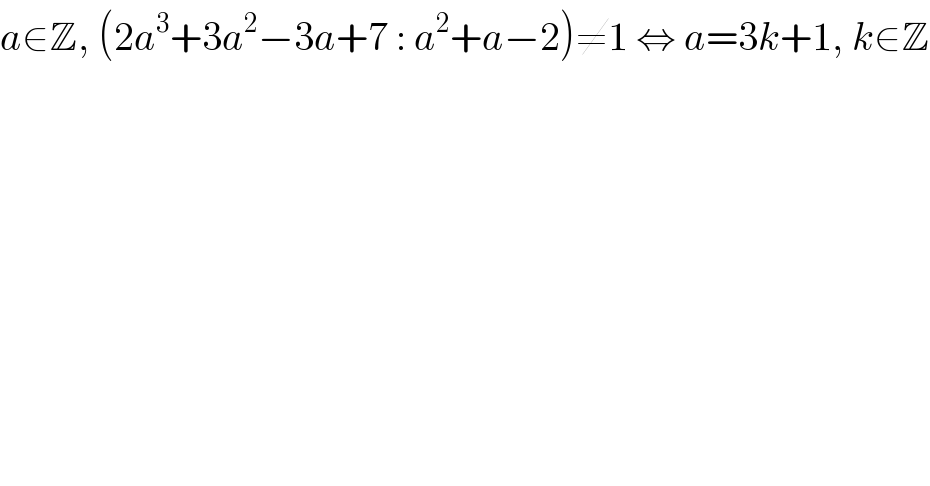
$${a}\in\mathbb{Z},\:\left(\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{3}{a}+\mathrm{7}\::\:{a}^{\mathrm{2}} +{a}−\mathrm{2}\right)\neq\mathrm{1}\:\Leftrightarrow\:{a}=\mathrm{3}{k}+\mathrm{1},\:{k}\in\mathbb{Z} \\ $$
Commented by Yozzii last updated on 30/Jul/16
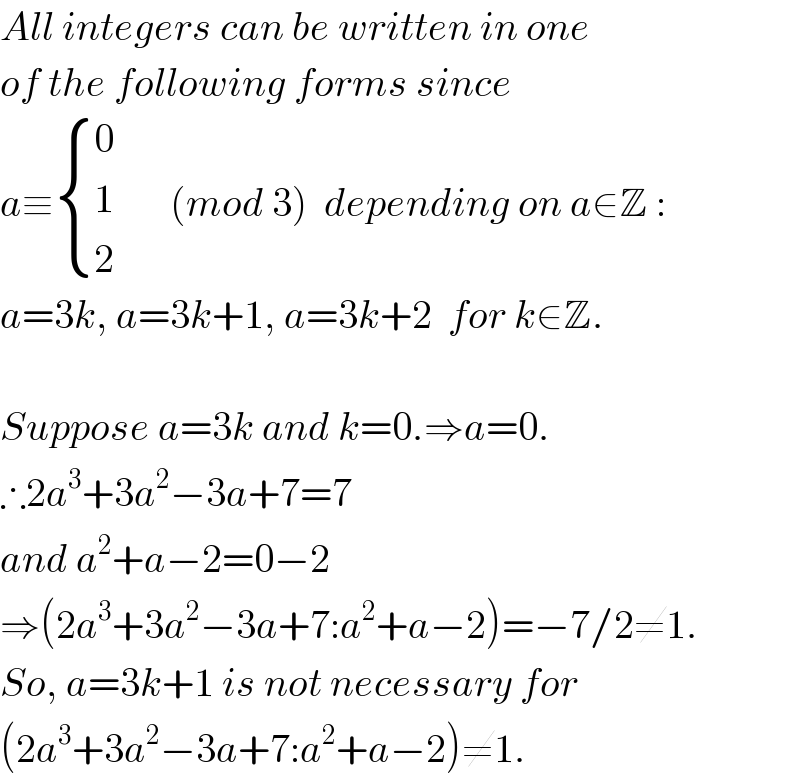
$${All}\:{integers}\:{can}\:{be}\:{written}\:{in}\:{one} \\ $$$${of}\:{the}\:{following}\:{forms}\:{since} \\ $$$${a}\equiv\begin{cases}{\mathrm{0}}\\{\mathrm{1}}\\{\mathrm{2}}\end{cases}\:\:\:\:\:\:\:\left({mod}\:\mathrm{3}\right)\:\:{depending}\:{on}\:{a}\in\mathbb{Z}\::\: \\ $$$${a}=\mathrm{3}{k},\:{a}=\mathrm{3}{k}+\mathrm{1},\:{a}=\mathrm{3}{k}+\mathrm{2}\:\:{for}\:{k}\in\mathbb{Z}. \\ $$$$ \\ $$$${Suppose}\:{a}=\mathrm{3}{k}\:{and}\:{k}=\mathrm{0}.\Rightarrow{a}=\mathrm{0}. \\ $$$$\therefore\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{3}{a}+\mathrm{7}=\mathrm{7} \\ $$$${and}\:{a}^{\mathrm{2}} +{a}−\mathrm{2}=\mathrm{0}−\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{3}{a}+\mathrm{7}:{a}^{\mathrm{2}} +{a}−\mathrm{2}\right)=−\mathrm{7}/\mathrm{2}\neq\mathrm{1}. \\ $$$${So},\:{a}=\mathrm{3}{k}+\mathrm{1}\:{is}\:{not}\:{necessary}\:{for} \\ $$$$\left(\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{3}{a}+\mathrm{7}:{a}^{\mathrm{2}} +{a}−\mathrm{2}\right)\neq\mathrm{1}. \\ $$
Commented by Tawakalitu. last updated on 30/Jul/16

$${Thanks}\:{sir} \\ $$
