
Question Number 68336 by pete last updated on 09/Sep/19
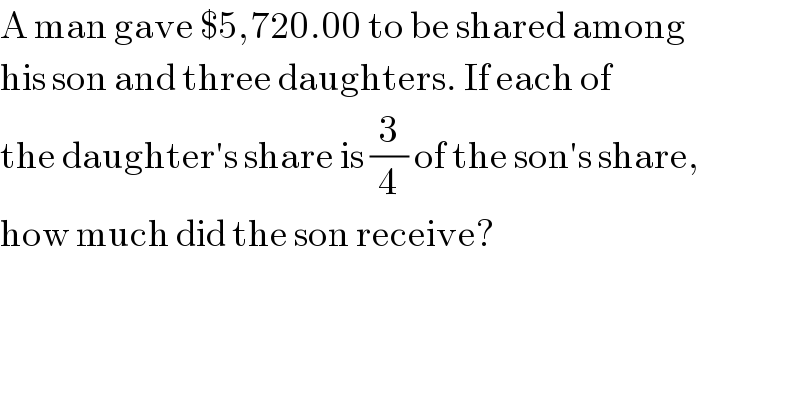
$$\mathrm{A}\:\mathrm{man}\:\mathrm{gave}\:\$\mathrm{5},\mathrm{720}.\mathrm{00}\:\mathrm{to}\:\mathrm{be}\:\mathrm{shared}\:\mathrm{among} \\ $$$$\mathrm{his}\:\mathrm{son}\:\mathrm{and}\:\mathrm{three}\:\mathrm{daughters}.\:\mathrm{If}\:\mathrm{each}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{daughter}'\mathrm{s}\:\mathrm{share}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{of}\:\mathrm{the}\:\mathrm{son}'\mathrm{s}\:\mathrm{share}, \\ $$$$\mathrm{how}\:\mathrm{much}\:\mathrm{did}\:\mathrm{the}\:\mathrm{son}\:\mathrm{receive}? \\ $$
Commented by Rasheed.Sindhi last updated on 09/Sep/19
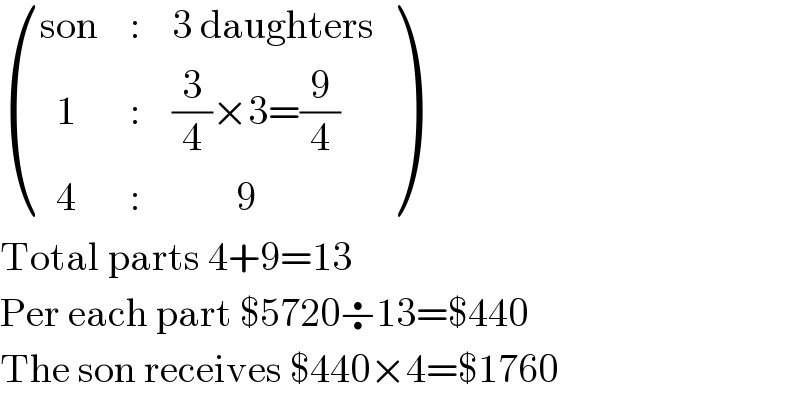
$$\begin{pmatrix}{\mathrm{son}}&{:}&{\mathrm{3}\:\mathrm{daughters}}\\{\:\:\mathrm{1}}&{:}&{\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{3}=\frac{\mathrm{9}}{\mathrm{4}}}\\{\:\:\mathrm{4}}&{:}&{\:\:\:\:\:\:\:\:\mathrm{9}}\end{pmatrix} \\ $$$$\mathrm{Total}\:\mathrm{parts}\:\mathrm{4}+\mathrm{9}=\mathrm{13} \\ $$$$\mathrm{Per}\:\mathrm{each}\:\mathrm{part}\:\$\mathrm{5720}\boldsymbol{\div}\mathrm{13}=\$\mathrm{440} \\ $$$$\mathrm{The}\:\mathrm{son}\:\mathrm{receives}\:\$\mathrm{440}×\mathrm{4}=\$\mathrm{1760} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/19
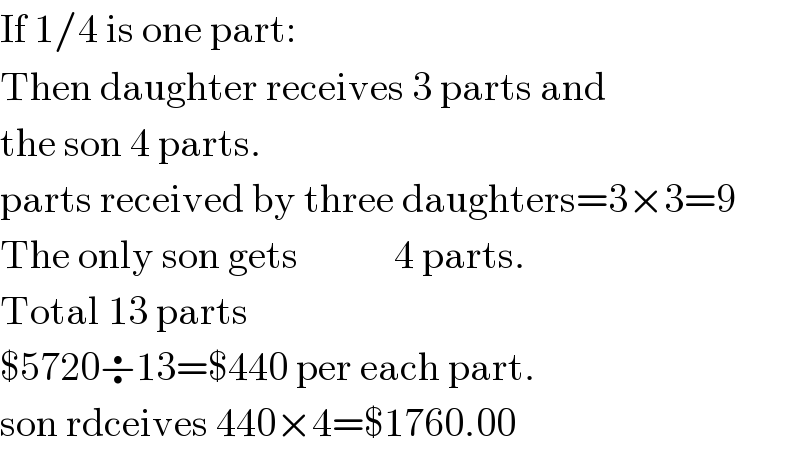
$$\mathrm{If}\:\mathrm{1}/\mathrm{4}\:\mathrm{is}\:\mathrm{one}\:\mathrm{part}: \\ $$$$\mathrm{Then}\:\mathrm{daughter}\:\mathrm{receives}\:\mathrm{3}\:\mathrm{parts}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{son}\:\mathrm{4}\:\mathrm{parts}. \\ $$$$\mathrm{parts}\:\mathrm{received}\:\mathrm{by}\:\mathrm{three}\:\mathrm{daughters}=\mathrm{3}×\mathrm{3}=\mathrm{9} \\ $$$$\mathrm{The}\:\mathrm{only}\:\mathrm{son}\:\mathrm{gets}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\mathrm{parts}. \\ $$$$\mathrm{Total}\:\mathrm{13}\:\mathrm{parts} \\ $$$$\$\mathrm{5720}\boldsymbol{\div}\mathrm{13}=\$\mathrm{440}\:\mathrm{per}\:\mathrm{each}\:\mathrm{part}. \\ $$$$\mathrm{son}\:\mathrm{rdceives}\:\mathrm{440}×\mathrm{4}=\$\mathrm{1760}.\mathrm{00} \\ $$
Commented by pete last updated on 10/Sep/19
$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Mr}.\:\mathrm{Rasheed} \\ $$
Commented by Rasheed.Sindhi last updated on 10/Sep/19
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{Mr}.\:\mathrm{Pete}! \\ $$
