
Question Number 68188 by mhmd last updated on 06/Sep/19

$$\sum_{{n}=\mathrm{3}} ^{\propto} \:\mathrm{1}/{n}\left({ln}\:{n}\right)^{\mathrm{2}} \:\:\:{is}\:{the}\:{function}\:{converg}\:{or}\:{diverg}\:?\:{pleas}\:{help}\:{me} \\ $$
Commented by Abdo msup. last updated on 07/Sep/19
![let ϕ(x) =(1/(x(lnx)^2 )) with x≥3 we have ϕ^′ (x) =−(((lnx)^2 +x ×((2lnx)/x))/(x^2 (lnx)^4 )) =−(((lnx)^2 ++2lnx)/(x^2 (lnx)^4 )) ⇒ ϕ^′ (x)<0 ⇒ϕ is increasing on [3,+∞[ so Σ_(n=3) ^∞ (1/(n(lnn)^2 )) and ∫_3 ^(+∞) (dx/(x(lnx)^2 )) have the same nsture of convervence changement lnx =t give ∫_3 ^(+∞) (dx/(x(lnx)^2 )) =∫_(ln(3)) ^(+∞) ((e^t dt)/(e^t t^2 ))dt =∫_(ln(3)) ^(+∞) (dt/t^2 ) =[−(1/t)]_(ln(3)) ^(+∞) =(1/(ln(3)))<+∞ ⇒this integral converges ⇒the serie converges.](Q68197.png)
$${let}\:\varphi\left({x}\right)\:=\frac{\mathrm{1}}{{x}\left({lnx}\right)^{\mathrm{2}} }\:\:{with}\:\:{x}\geqslant\mathrm{3}\:\:{we}\:{have} \\ $$$$\varphi^{'} \left({x}\right)\:=−\frac{\left({lnx}\right)^{\mathrm{2}} +{x}\:×\frac{\mathrm{2}{lnx}}{{x}}}{{x}^{\mathrm{2}} \left({lnx}\right)^{\mathrm{4}} }\:=−\frac{\left({lnx}\right)^{\mathrm{2}} \:++\mathrm{2}{lnx}}{{x}^{\mathrm{2}} \left({lnx}\right)^{\mathrm{4}} }\:\Rightarrow \\ $$$$\varphi^{'} \left({x}\right)<\mathrm{0}\:\Rightarrow\varphi\:{is}\:{increasing}\:{on}\:\left[\mathrm{3},+\infty\left[\right.\right. \\ $$$${so}\:\:\sum_{{n}=\mathrm{3}} ^{\infty} \:\frac{\mathrm{1}}{{n}\left({lnn}\right)^{\mathrm{2}} }\:{and}\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\frac{{dx}}{{x}\left({lnx}\right)^{\mathrm{2}} }\:{have}\:{the}\:{same} \\ $$$${nsture}\:{of}\:{convervence}\:\:{changement}\:{lnx}\:={t}\:{give} \\ $$$$\int_{\mathrm{3}} ^{+\infty} \:\:\frac{{dx}}{{x}\left({lnx}\right)^{\mathrm{2}} }\:=\int_{{ln}\left(\mathrm{3}\right)} ^{+\infty} \:\:\frac{{e}^{{t}} {dt}}{{e}^{{t}} {t}^{\mathrm{2}} }{dt}\:=\int_{{ln}\left(\mathrm{3}\right)} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$=\left[−\frac{\mathrm{1}}{{t}}\right]_{{ln}\left(\mathrm{3}\right)} ^{+\infty} \:=\frac{\mathrm{1}}{{ln}\left(\mathrm{3}\right)}<+\infty\:\Rightarrow{this}\:{integral}\:{converges} \\ $$$$\Rightarrow{the}\:{serie}\:\:{converges}. \\ $$
Commented by Abdo msup. last updated on 07/Sep/19
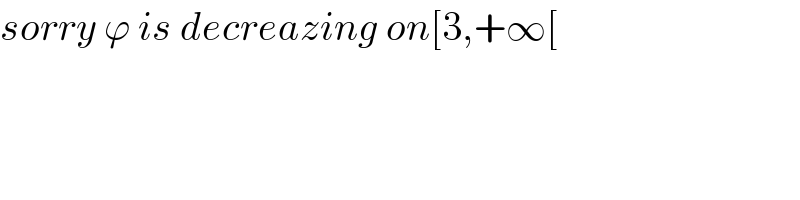
$${sorry}\:\varphi\:{is}\:{decreazing}\:{on}\left[\mathrm{3},+\infty\left[\right.\right. \\ $$
