
Question Number 68178 by Mikael last updated on 06/Sep/19
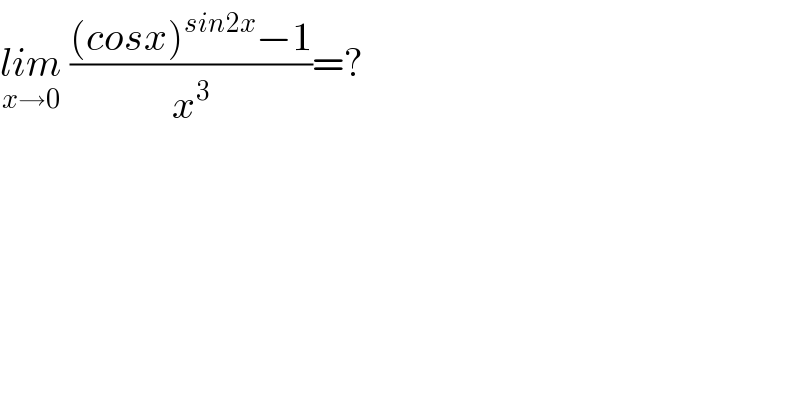
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\left({cosx}\right)^{{sin}\mathrm{2}{x}} −\mathrm{1}}{{x}^{\mathrm{3}} }=? \\ $$
Commented by mathmax by abdo last updated on 06/Sep/19
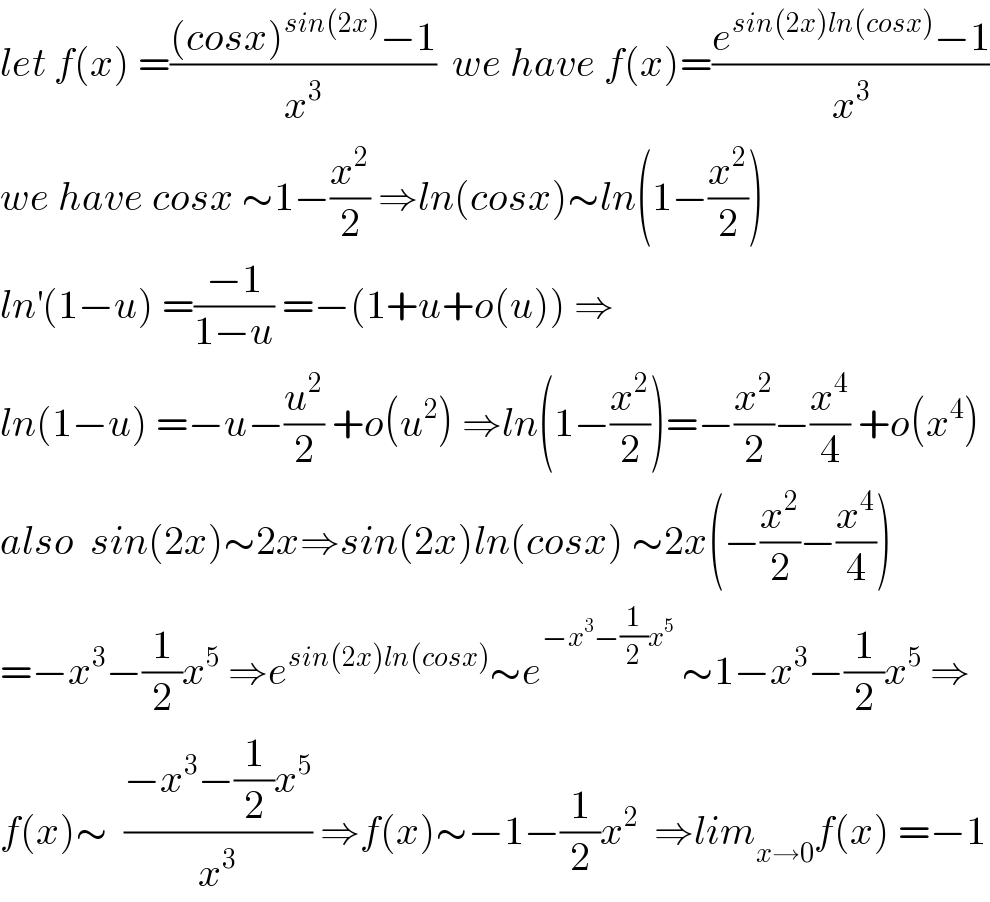
$${let}\:{f}\left({x}\right)\:=\frac{\left({cosx}\right)^{{sin}\left(\mathrm{2}{x}\right)} −\mathrm{1}}{{x}^{\mathrm{3}} }\:\:{we}\:{have}\:{f}\left({x}\right)=\frac{{e}^{{sin}\left(\mathrm{2}{x}\right){ln}\left({cosx}\right)} −\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$${we}\:{have}\:{cosx}\:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{ln}\left({cosx}\right)\sim{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$${ln}^{'} \left(\mathrm{1}−{u}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−{u}}\:=−\left(\mathrm{1}+{u}+{o}\left({u}\right)\right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{u}\right)\:=−{u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:+{o}\left({x}^{\mathrm{4}} \right) \\ $$$${also}\:\:{sin}\left(\mathrm{2}{x}\right)\sim\mathrm{2}{x}\Rightarrow{sin}\left(\mathrm{2}{x}\right){ln}\left({cosx}\right)\:\sim\mathrm{2}{x}\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right) \\ $$$$=−{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} \:\Rightarrow{e}^{{sin}\left(\mathrm{2}{x}\right){ln}\left({cosx}\right)} \sim{e}^{−{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} } \:\sim\mathrm{1}−{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} \:\Rightarrow \\ $$$${f}\left({x}\right)\sim\:\:\frac{−{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} }{{x}^{\mathrm{3}} }\:\Rightarrow{f}\left({x}\right)\sim−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)\:=−\mathrm{1} \\ $$
Commented by Mikael last updated on 06/Sep/19

$${thank}\:{you}. \\ $$
