
Question Number 6811 by Tawakalitu. last updated on 28/Jul/16
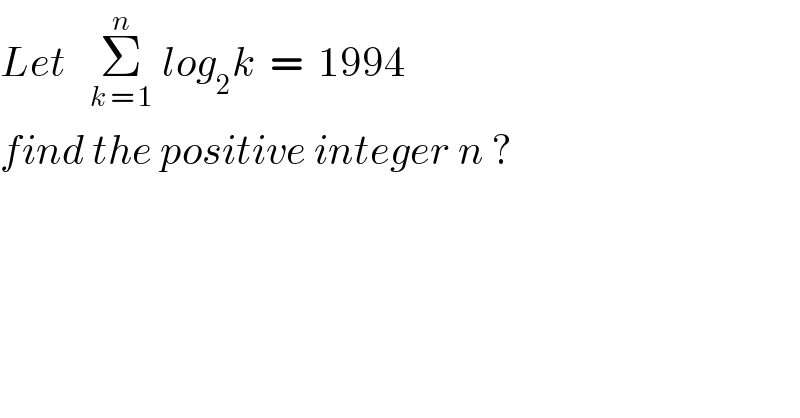
$${Let}\:\:\:\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\:{log}_{\mathrm{2}} {k}\:\:=\:\:\mathrm{1994} \\ $$$${find}\:{the}\:{positive}\:{integer}\:{n}\:? \\ $$
Commented by Yozzii last updated on 29/Jul/16
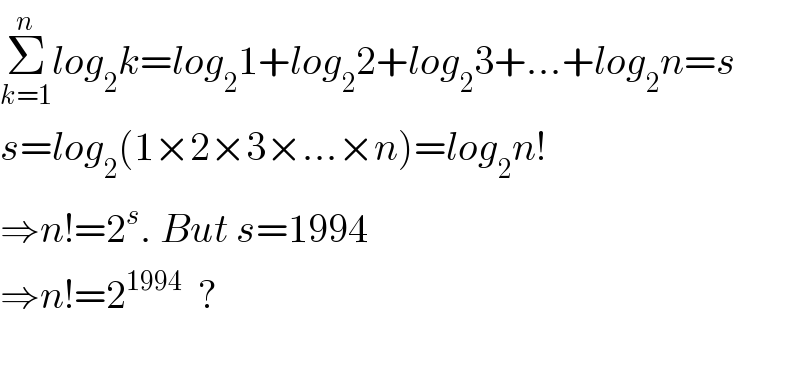
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{log}_{\mathrm{2}} {k}={log}_{\mathrm{2}} \mathrm{1}+{log}_{\mathrm{2}} \mathrm{2}+{log}_{\mathrm{2}} \mathrm{3}+...+{log}_{\mathrm{2}} {n}={s} \\ $$$${s}={log}_{\mathrm{2}} \left(\mathrm{1}×\mathrm{2}×\mathrm{3}×...×{n}\right)={log}_{\mathrm{2}} {n}! \\ $$$$\Rightarrow{n}!=\mathrm{2}^{{s}} .\:{But}\:{s}=\mathrm{1994} \\ $$$$\Rightarrow{n}!=\mathrm{2}^{\mathrm{1994}} \:\:? \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 29/Jul/16
$${Thanks}\:{so}\:{much}... \\ $$$$ \\ $$$${please}\:{is}\:{that}\:{where}\:{i}\:{will}\:{stop}\:? \\ $$
Commented by Yozzii last updated on 29/Jul/16

$${If}\:{n}=\mathrm{2}\Rightarrow\:{n}!\:{has}\:{only}\:{the}\:{prime}\:\mathrm{2}\:{in} \\ $$$${its}\:{prime}\:{factorisation}.\:{If}\:{n}\geqslant\mathrm{3},\:\mathrm{3}\:{must} \\ $$$${appear}\:{in}\:{the}\:{prime}\:{factorisation}\:{of} \\ $$$${n}!\:{with}\:{the}\:{power}\:{of}\:\mathrm{3}\:{being}\:{at}\:{least}\:{one}. \\ $$$${n}\geqslant\mathrm{3}\Rightarrow{n}!=\mathrm{1}×\mathrm{2}×\mathrm{3}×\left\{\mathrm{4}×\mathrm{5}×...×{n}\right\} \\ $$$${or}\:\mathrm{3}\:{divides}\:{n}!.\:{This}\:{is}\:{for}\:{n}\in\mathbb{N}.\: \\ $$$${In}\:{this}\:{problem},\:{n}\in\mathbb{N}.\:{We}\:{found}\:{that}\: \\ $$$${n}!=\mathrm{2}^{\mathrm{1994}} \ggg\mathrm{6}=\mathrm{3}!\Rightarrow{n}\:{is}\:{at}\:{least}\:\mathrm{3}.\:{But}, \\ $$$${if}\:{n}\in\mathbb{N}\:{is}\:{at}\:{least}\:\mathrm{3}\:\Rightarrow\:\mathrm{3}\mid{n}!.\:{However}, \\ $$$$\mathrm{3}\:{does}\:{not}\:{divide}\:\mathrm{2}^{\mathrm{1994}} \:{or}\:\mathrm{3}\nmid{n}!\:{while}\: \\ $$$${min}\left({n}\right)=\mathrm{3}.\:{So},\:{no}\:{integer}\:{n}\:{exists}\:{satisfying} \\ $$$${n}!=\mathrm{2}^{\mathrm{1994}} .\: \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 29/Jul/16
$${I}\:{now}\:{understand}\:{better},\:{thanks}\:{so}\:{much}. \\ $$$$ \\ $$
