
Question Number 67963 by mhmd last updated on 02/Sep/19
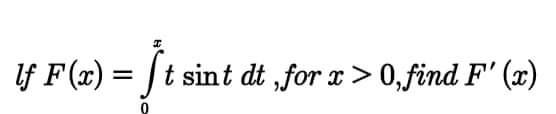
Commented by mathmax by abdo last updated on 02/Sep/19
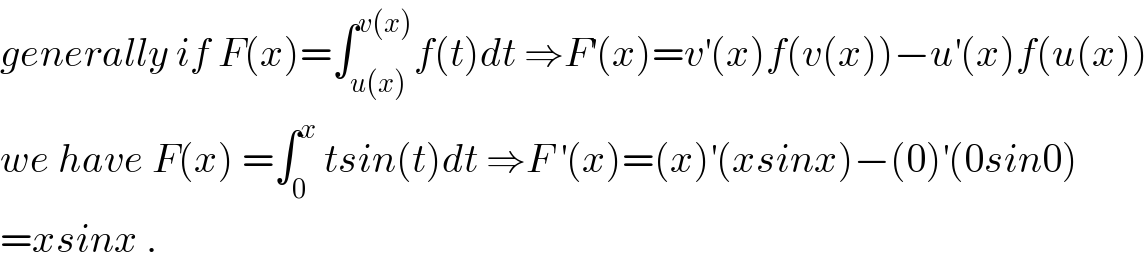
$${generally}\:{if}\:{F}\left({x}\right)=\int_{{u}\left({x}\right)} ^{{v}\left({x}\right)} {f}\left({t}\right){dt}\:\Rightarrow{F}^{'} \left({x}\right)={v}^{'} \left({x}\right){f}\left({v}\left({x}\right)\right)−{u}^{'} \left({x}\right){f}\left({u}\left({x}\right)\right) \\ $$$${we}\:{have}\:{F}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:{tsin}\left({t}\right){dt}\:\Rightarrow{F}\:^{'} \left({x}\right)=\left({x}\right)^{'} \left({xsinx}\right)−\left(\mathrm{0}\right)^{'} \left(\mathrm{0}{sin}\mathrm{0}\right) \\ $$$$={xsinx}\:. \\ $$
Answered by mr W last updated on 02/Sep/19
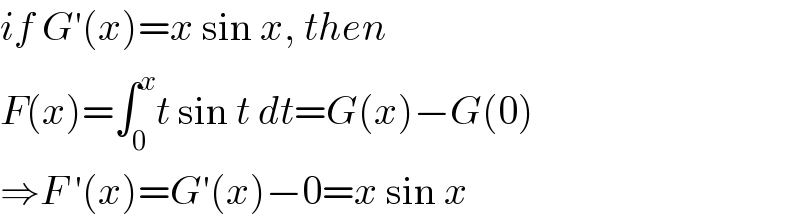
$${if}\:{G}'\left({x}\right)={x}\:\mathrm{sin}\:{x},\:{then} \\ $$$${F}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} {t}\:\mathrm{sin}\:{t}\:{dt}={G}\left({x}\right)−{G}\left(\mathrm{0}\right) \\ $$$$\Rightarrow{F}\:'\left({x}\right)={G}'\left({x}\right)−\mathrm{0}={x}\:\mathrm{sin}\:{x} \\ $$
