
Question Number 67851 by mathmax by abdo last updated on 01/Sep/19
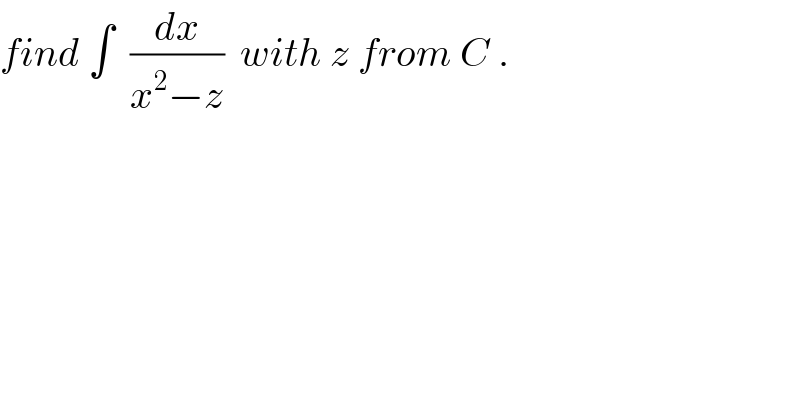
$${find}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{with}\:{z}\:{from}\:{C}\:. \\ $$
Commented by MJS last updated on 01/Sep/19
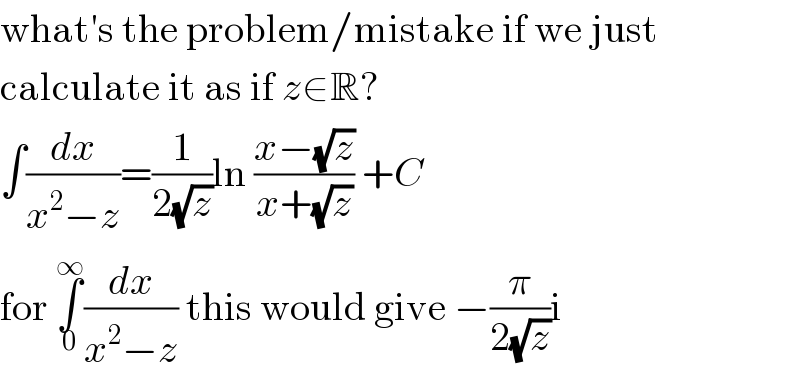
$$\mathrm{what}'\mathrm{s}\:\mathrm{the}\:\mathrm{problem}/\mathrm{mistake}\:\mathrm{if}\:\mathrm{we}\:\mathrm{just} \\ $$$$\mathrm{calculate}\:\mathrm{it}\:\mathrm{as}\:\mathrm{if}\:{z}\in\mathbb{R}? \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −{z}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{z}}}\mathrm{ln}\:\frac{{x}−\sqrt{{z}}}{{x}+\sqrt{{z}}}\:+{C} \\ $$$$\mathrm{for}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\mathrm{this}\:\mathrm{would}\:\mathrm{give}\:−\frac{\pi}{\mathrm{2}\sqrt{{z}}}\mathrm{i} \\ $$
Commented by mathmax by abdo last updated on 01/Sep/19
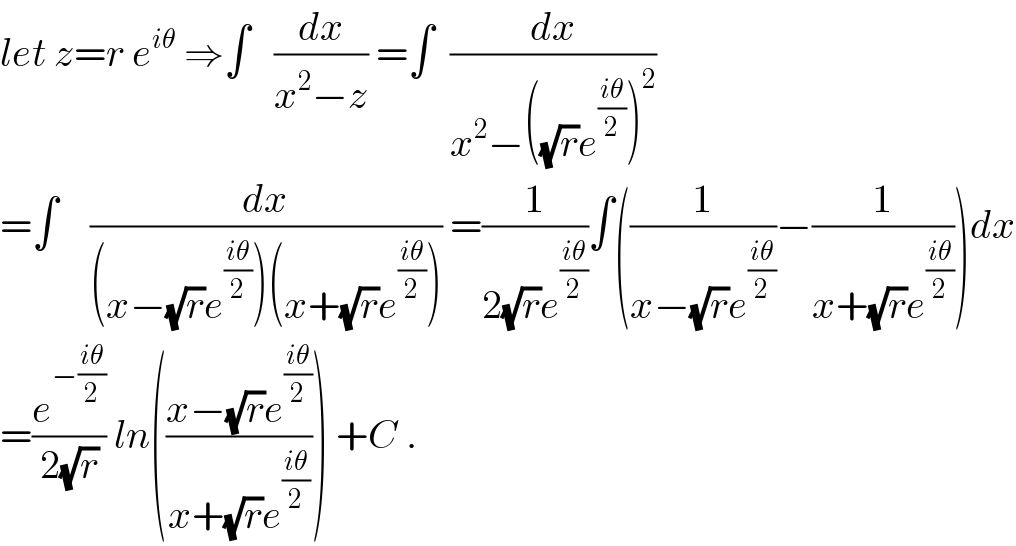
$${let}\:{z}={r}\:{e}^{{i}\theta} \:\Rightarrow\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\left(\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)^{\mathrm{2}} } \\ $$$$=\int\:\:\:\:\frac{{dx}}{\left({x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)\left({x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\int\left(\frac{\mathrm{1}}{{x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }−\frac{\mathrm{1}}{{x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\right){dx} \\ $$$$=\frac{{e}^{−\frac{{i}\theta}{\mathrm{2}}} }{\mathrm{2}\sqrt{{r}}}\:{ln}\left(\frac{{x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }{{x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\right)\:+{C}\:. \\ $$
Commented by mathmax by abdo last updated on 01/Sep/19
$${sir}\:{mjs}\:{your}\:{answer}\:{is}\:{correct}\:. \\ $$
Commented by mathmax by abdo last updated on 01/Sep/19
![∫_0 ^∞ (dx/(x^2 −z)) =(e^(−((iθ)/2)) /(2(√r)))[ln(((x−(√r)e^((iθ)/2) )/(x+(√r)e^((iθ)/2) )))]_0 ^(+∞) =(e^(−((iθ)/2)) /(2(√r)))(−ln(−1)) =((iπ)/(2(2(√r))e^((iθ)/2) )) =((iπ)/(4(√r)e^((iθ)/2) )) with z =r e^(iθ) .](Q67896.png)
$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:=\frac{{e}^{−\frac{{i}\theta}{\mathrm{2}}} }{\mathrm{2}\sqrt{{r}}}\left[{ln}\left(\frac{{x}−\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }{{x}+\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\right)\right]_{\mathrm{0}} ^{+\infty} =\frac{{e}^{−\frac{{i}\theta}{\mathrm{2}}} }{\mathrm{2}\sqrt{{r}}}\left(−{ln}\left(−\mathrm{1}\right)\right)\:=\frac{{i}\pi}{\mathrm{2}\left(\mathrm{2}\sqrt{{r}}\right){e}^{\frac{{i}\theta}{\mathrm{2}}} } \\ $$$$=\frac{{i}\pi}{\mathrm{4}\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} }\:\:\:{with}\:{z}\:={r}\:{e}^{{i}\theta} \:. \\ $$
Commented by MJS last updated on 01/Sep/19
$$\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{wasn}'\mathrm{t}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{this}\:\mathrm{was}\:\mathrm{allowed}\:\mathrm{in}\:\mathbb{C} \\ $$
