
Question Number 67849 by mr W last updated on 01/Sep/19

Commented by MJS last updated on 01/Sep/19

$$\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{in}\:\mathrm{the}\:\mathrm{center}\:\mathrm{90}°? \\ $$
Commented by mr W last updated on 01/Sep/19

$${not}\:{given}. \\ $$
Commented by Prithwish sen last updated on 01/Sep/19
Commented by Prithwish sen last updated on 01/Sep/19

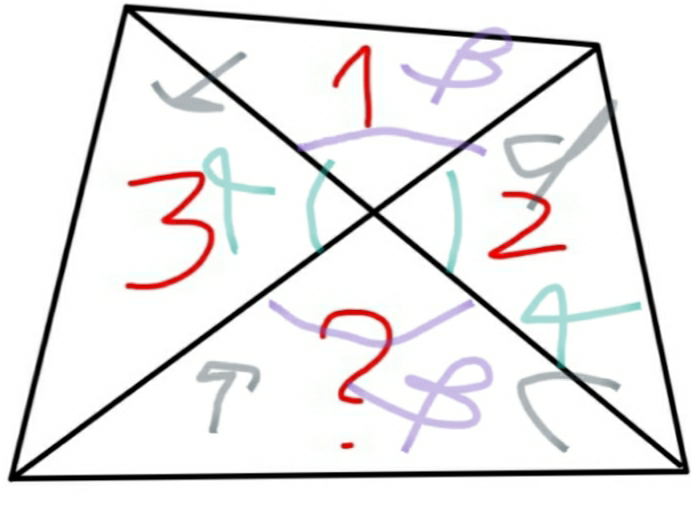
$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{absin}\alpha=\mathrm{3}...\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cdsin}\alpha=\mathrm{2}....\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{bdsin}\beta=\mathrm{1}...\left(\mathrm{iii}\right) \\ $$$$\mathrm{find}\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{acsin}\beta \\ $$
Commented by MJS last updated on 01/Sep/19

$$\mathrm{sin}\:\beta\:=\mathrm{sin}\:\alpha \\ $$
Commented by mr W last updated on 01/Sep/19
$${thanks}\:{sirs}! \\ $$$${i}\:{used}\:{the}\:{same}\:{method}. \\ $$
Commented by Prithwish sen last updated on 01/Sep/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{alot}. \\ $$
Answered by mr W last updated on 01/Sep/19
Commented by mr W last updated on 01/Sep/19
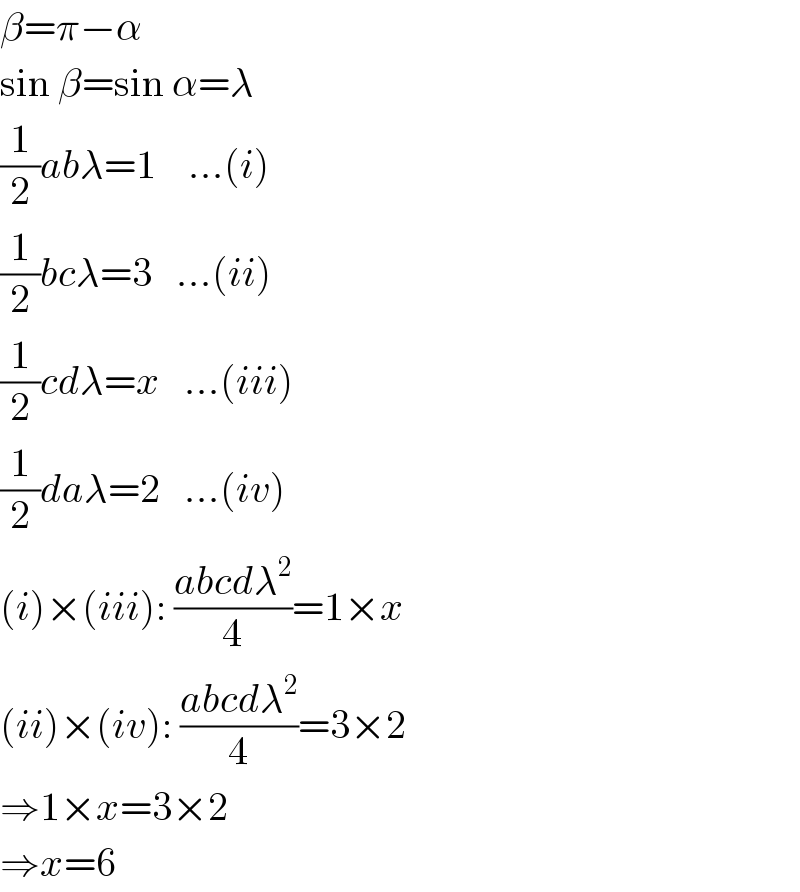
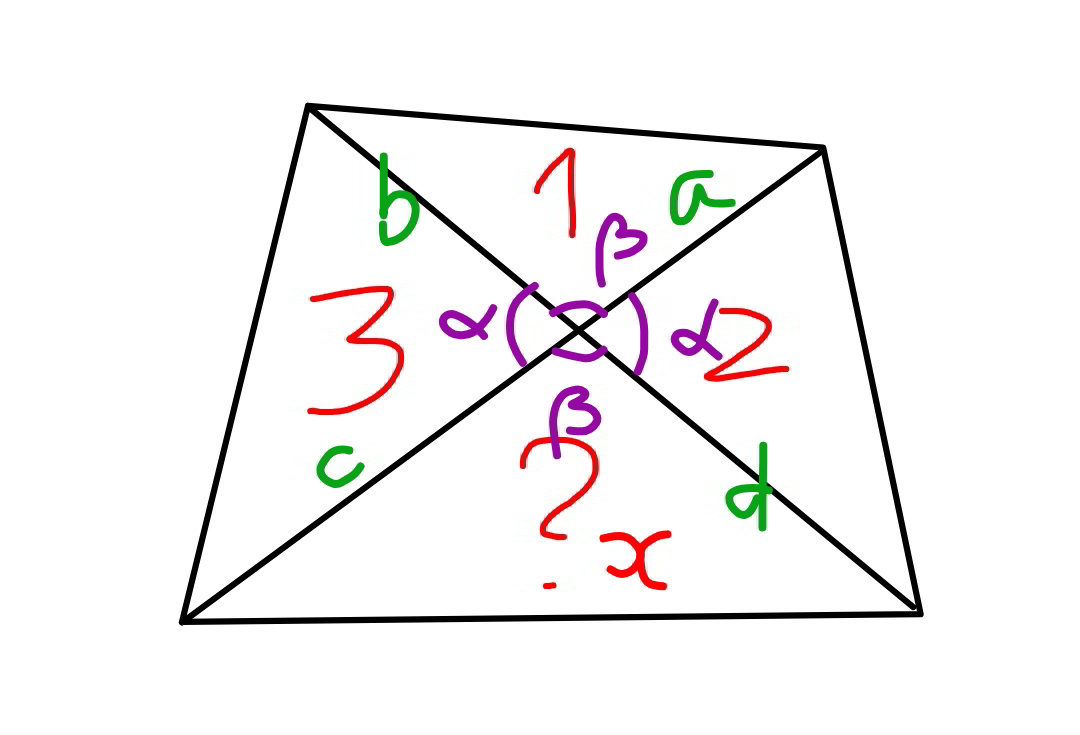
$$\beta=\pi−\alpha \\ $$$$\mathrm{sin}\:\beta=\mathrm{sin}\:\alpha=\lambda \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ab}\lambda=\mathrm{1}\:\:\:\:...\left({i}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{bc}\lambda=\mathrm{3}\:\:\:...\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{cd}\lambda={x}\:\:\:...\left({iii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{da}\lambda=\mathrm{2}\:\:\:...\left({iv}\right) \\ $$$$\left({i}\right)×\left({iii}\right):\:\frac{{abcd}\lambda^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1}×{x} \\ $$$$\left({ii}\right)×\left({iv}\right):\:\frac{{abcd}\lambda^{\mathrm{2}} }{\mathrm{4}}=\mathrm{3}×\mathrm{2} \\ $$$$\Rightarrow\mathrm{1}×{x}=\mathrm{3}×\mathrm{2} \\ $$$$\Rightarrow{x}=\mathrm{6} \\ $$
