
Question Number 67799 by mathmax by abdo last updated on 31/Aug/19
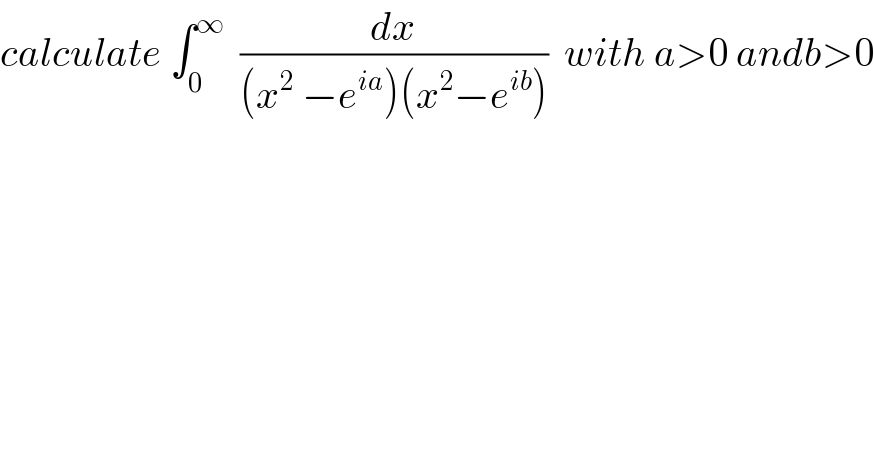
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:−{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)}\:\:{with}\:{a}>\mathrm{0}\:{andb}>\mathrm{0} \\ $$
Commented byMJS last updated on 31/Aug/19
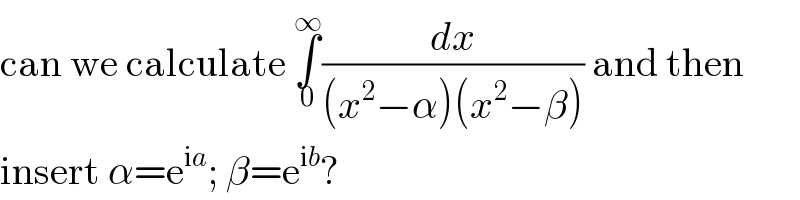
$$\mathrm{can}\:\mathrm{we}\:\mathrm{calculate}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{\left({x}^{\mathrm{2}} −\alpha\right)\left({x}^{\mathrm{2}} −\beta\right)}\:\mathrm{and}\:\mathrm{then} \\ $$ $$\mathrm{insert}\:\alpha=\mathrm{e}^{\mathrm{i}{a}} ;\:\beta=\mathrm{e}^{\mathrm{i}{b}} ? \\ $$
Commented bymathmax by abdo last updated on 31/Aug/19
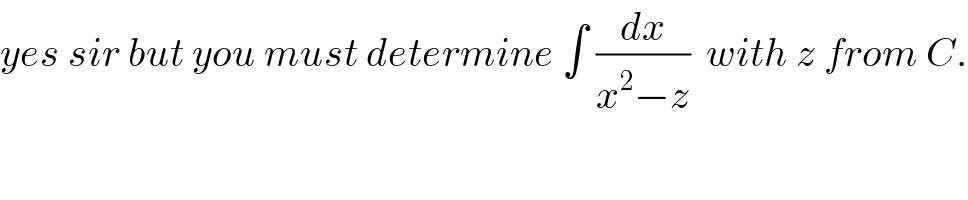
$${yes}\:{sir}\:{but}\:{you}\:{must}\:{determine}\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} −{z}}\:\:{with}\:{z}\:{from}\:{C}. \\ $$
Commented bymathmax by abdo last updated on 01/Sep/19

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)}\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)} \\ $$ $${let}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −{e}^{{ia}} \right)\left({z}^{\mathrm{2}} −{e}^{{ib}} \right)}\:\Rightarrow\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{e}^{\frac{{ia}}{\mathrm{2}}} \right)\left({z}+{e}^{\frac{{ia}}{\mathrm{2}}} \right)\left({z}−{e}^{\frac{{ib}}{\mathrm{2}}} \right)\left({z}+{e}^{\frac{{ib}}{\mathrm{2}}} \right)} \\ $$ $${the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{ia}}{\mathrm{2}}} \:{and}\:\overset{−} {+}{e}^{\frac{{ib}}{\mathrm{2}\:}} \:\:\:{residus}\:{theorem}\:{give} \\ $$ $$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{ia}}{\mathrm{2}}} \right)+{Res}\left(\varphi,{e}^{\frac{{ib}}{\mathrm{2}}} \right)\right\} \\ $$ $${Res}\left(\varphi,{e}^{\frac{{ia}}{\mathrm{2}}} \right)={lim}_{{z}\rightarrow{e}^{\frac{{ia}}{\mathrm{2}}} } \:\:\left({z}−{e}^{\frac{{ia}}{\mathrm{2}}} \right)\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{e}^{\frac{{ia}}{\mathrm{2}}} \left({e}^{{ia}} −{e}^{{ib}} \right)}\:=\frac{{e}^{−{i}\frac{{a}}{\mathrm{2}}} }{\mathrm{2}\left({e}^{{ia}} −{e}^{{ib}} \right)} \\ $$ $${Res}\left(\varphi,{e}^{\frac{{ib}}{\mathrm{2}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{ib}}{\mathrm{2}}} } \:\:\left({z}−{e}^{\frac{{ib}}{\mathrm{2}}} \right)\varphi\left({z}\right)\:=\frac{{e}^{−\frac{{ib}}{\mathrm{2}}} }{\mathrm{2}\left({e}^{{ib}} \:−{e}^{{ia}} \right)}\:\Rightarrow \\ $$ $$\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{2}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{{e}^{−\frac{{ia}}{\mathrm{2}}} }{\mathrm{2}\left({e}^{{ia}} −{e}^{{ib}} \right)}\:+\frac{{e}^{−\frac{{ib}}{\mathrm{2}}} }{\mathrm{2}\left({e}^{{ib}} −{e}^{{ia}} \right)}\right\} \\ $$ $$ \\ $$ $$=\frac{{i}\pi}{{e}^{{ia}} −{e}^{{ib}} }\left\{\:{e}^{−\frac{{ia}}{\mathrm{2}}} −{e}^{−\frac{{ib}}{\mathrm{2}}} \right\}\:=\mathrm{2}{I}\:\Rightarrow \\ $$ $${I}\:=\frac{{i}\pi\left({e}^{−\frac{{ia}}{\mathrm{2}}} −{e}^{−\frac{{ib}}{\mathrm{2}}} \right)}{\mathrm{2}\left({e}^{{ia}} −{e}^{{ib}} \right)}. \\ $$
Answered by mind is power last updated on 01/Sep/19
![let γ_r ={z∈C such that∣z∣≤r ∣im(z)>0} we have ∫_0 ^(+∞) (dx/((x^2 −e^(ia) )(x^2 −e^(ib) )))=(1/2)∫_(−∞) ^(+∞) (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) let f(z)=(1/((z^2 −e^(ia) )(z^2 −e^(ib) ))) f(z)=(1/((r^2 e^(2i∅) −e^(ia) )(r^2 e^(2i∅) −e^(ib) ))) over γ_r ∣f(z)∣≤(1/(∣r^2 −1∣^2 )) we used ∣z+z′∣≥∣∣z∣−∣z′∣∣ twice ⇒∫_(γr) f(z)dz≤∫_γ_r (1/((r^2 −1)^2 ))dz=((πr)/((r^2 −1)^2 ))→0=as r→+∞ residu theorem poles of f inside γ_r ∪]−∞.+∞[ ar e^(i(a/2)) .e^((ib)/2) lim (z−e^(i(a/2)) ).f(z)=(1/(2e^(i(a/2)) .(e^(ia) −e^(ib) ))) lim(z−e^(i(b/2)) )f(z)=(1/(2e^(i(b/2)) (e^(ib) −e^(ia) ))) ∫_(−∞) ^(+∞) f(z)dz=2iπΣ_(residu) f(z)=2iπ((e^(−i(b/2)) /((e^(ib) −e^(ia) )2))−(e^(−((ia)/2)) /(2(e^(ib) −e^(ia) )))) =iπ(((e^(−((ib)/2)) −e^((−ia)/2) )/((e^(i((a+b)/2)) (e^(i((b−a)/2)) −e^(i−((b−a)/2)) ))))=iπ((e^(−ib−i(a/2)) −e^(−ia−i(b/2)) )/(2isin(((a−b)/2))))](Q67829.png)
$${let}\:\gamma_{{r}} =\left\{{z}\in{C}\:\:{such}\:{that}\mid{z}\mid\leqslant{r}\:\mid{im}\left({z}\right)>\mathrm{0}\right\} \\ $$ $${we}\:{have}\:\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} −{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} −{e}^{{ia}} \right)\left({x}^{\mathrm{2}} −{e}^{{ib}} \right)} \\ $$ $${let}\:{f}\left({z}\right)=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −{e}^{{ia}} \right)\left({z}^{\mathrm{2}} −{e}^{{ib}} \right)} \\ $$ $${f}\left({z}\right)=\frac{\mathrm{1}}{\left({r}^{\mathrm{2}} {e}^{\mathrm{2}{i}\emptyset} −{e}^{{ia}} \right)\left({r}^{\mathrm{2}} {e}^{\mathrm{2}{i}\emptyset} −{e}^{{ib}} \right)}\:\:{over}\:\gamma_{{r}} \\ $$ $$\mid{f}\left({z}\right)\mid\leqslant\frac{\mathrm{1}}{\mid{r}^{\mathrm{2}} −\mathrm{1}\mid^{\mathrm{2}} } \\ $$ $${we}\:{used}\:\mid{z}+{z}'\mid\geqslant\mid\mid{z}\mid−\mid{z}'\mid\mid\:{twice} \\ $$ $$\Rightarrow\int_{\gamma{r}} {f}\left({z}\right){dz}\leqslant\int_{\gamma_{{r}} } \frac{\mathrm{1}}{\left({r}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dz}=\frac{\pi{r}}{\left({r}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\rightarrow\mathrm{0}={as}\:{r}\rightarrow+\infty \\ $$ $${residu}\:{theorem} \\ $$ $$\left.{poles}\:{of}\:{f}\:{inside}\:\gamma_{{r}} \cup\right]−\infty.+\infty\left[\:{ar}\:{e}^{{i}\frac{{a}}{\mathrm{2}}} .{e}^{\frac{{ib}}{\mathrm{2}}} \right. \\ $$ $${lim}\:\left({z}−{e}^{{i}\frac{{a}}{\mathrm{2}}} \right).{f}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}{e}^{{i}\frac{{a}}{\mathrm{2}}} .\left({e}^{{ia}} −{e}^{{ib}} \right)} \\ $$ $${lim}\left({z}−{e}^{{i}\frac{{b}}{\mathrm{2}}} \right){f}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}{e}^{{i}\frac{{b}}{\mathrm{2}}} \left({e}^{{ib}} −{e}^{{ia}} \right)} \\ $$ $$\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi\sum_{{residu}} {f}\left({z}\right)=\mathrm{2}{i}\pi\left(\frac{{e}^{−{i}\frac{{b}}{\mathrm{2}}} }{\left({e}^{{ib}} −{e}^{{ia}} \right)\mathrm{2}}−\frac{{e}^{−\frac{{ia}}{\mathrm{2}}} }{\mathrm{2}\left({e}^{{ib}} −{e}^{{ia}} \right)}\right) \\ $$ $$={i}\pi\left(\frac{{e}^{−\frac{{ib}}{\mathrm{2}}} −{e}^{\frac{−{ia}}{\mathrm{2}}} }{\left({e}^{{i}\frac{{a}+{b}}{\mathrm{2}}} \left({e}^{{i}\frac{{b}−{a}}{\mathrm{2}}} −{e}^{{i}−\frac{{b}−{a}}{\mathrm{2}}} \right)\right.}\right)={i}\pi\frac{{e}^{−{ib}−{i}\frac{{a}}{\mathrm{2}}} −{e}^{−{ia}−{i}\frac{{b}}{\mathrm{2}}} }{\mathrm{2}{isin}\left(\frac{{a}−{b}}{\mathrm{2}}\right)} \\ $$ $$ \\ $$
Commented bymathmax by abdo last updated on 01/Sep/19

$${thank}\:{you}\:{sir}. \\ $$
Commented bymind is power last updated on 01/Sep/19

$${y}:{re}\:{welcom} \\ $$ $$ \\ $$
