
Question Number 67631 by Hassen_Timol last updated on 29/Aug/19

$$ \\ $$$$ \\ $$$$\:\:\:\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{tell}\:\mathrm{me},\:\mathrm{where}\:\mathrm{does}\:\mathrm{this}\: \\ $$$$\:\:\:\mathrm{formula}\:\mathrm{come}\:\mathrm{from}? \\ $$$$\:\:\:\mathrm{And}\:\mathrm{what}\:\mathrm{means}\:\mathrm{the}\:\mathrm{factorial}\:\mathrm{of}\:\mathrm{a}\:\mathrm{non}- \\ $$$$\:\:\:\mathrm{integer}\:\mathrm{number}? \\ $$$$ \\ $$$$\:\:\:\:\:\:\pi\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}!\right)^{\mathrm{2}} ×\:\mathrm{4} \\ $$$$ \\ $$$$\:\:\:{I}'{ve}\:{verified}\:{the}\:{above}\:{equation}\:{with}\:{calculator}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Thank}\:\mathrm{you} \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19
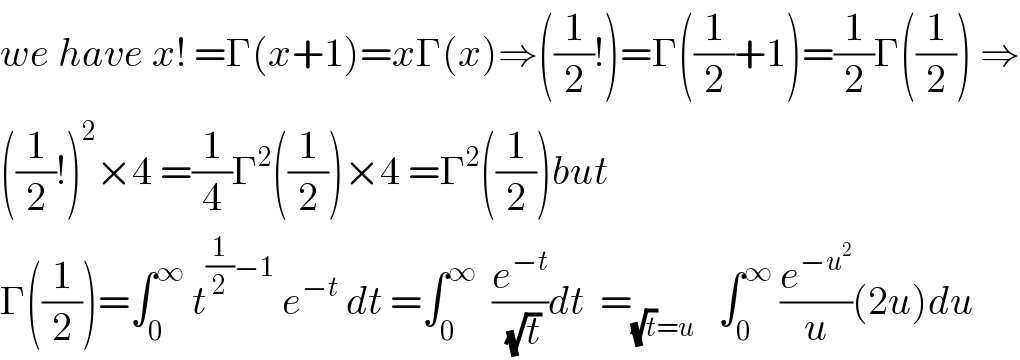
$${we}\:{have}\:{x}!\:=\Gamma\left({x}+\mathrm{1}\right)={x}\Gamma\left({x}\right)\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}}!\right)=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}!\right)^{\mathrm{2}} ×\mathrm{4}\:=\frac{\mathrm{1}}{\mathrm{4}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\mathrm{4}\:=\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right){but} \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} }{\sqrt{{t}}}{dt}\:\:=_{\sqrt{{t}}={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{u}^{\mathrm{2}} } }{{u}}\left(\mathrm{2}{u}\right){du} \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19
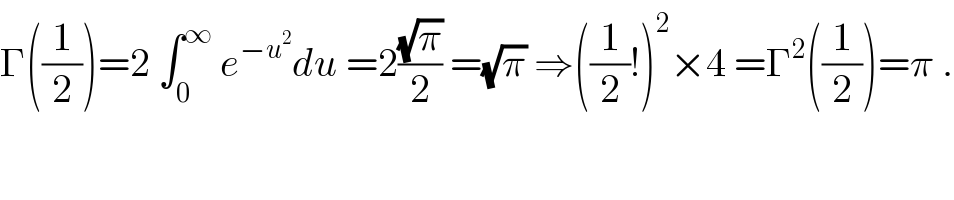
$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } {du}\:=\mathrm{2}\frac{\sqrt{\pi}}{\mathrm{2}}\:=\sqrt{\pi}\:\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}}!\right)^{\mathrm{2}} ×\mathrm{4}\:=\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\pi\:. \\ $$
Commented by Hassen_Timol last updated on 03/Sep/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}. \\ $$$$\mathrm{But}\:\mathrm{what}\:\mathrm{means}\:\mathrm{the}\:\Gamma\left({x}\right)\:\mathrm{function}\:\mathrm{and}\:\mathrm{how} \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{related}\:\mathrm{to}\:\mathrm{the}\:{x}!\:\mathrm{function}? \\ $$
