
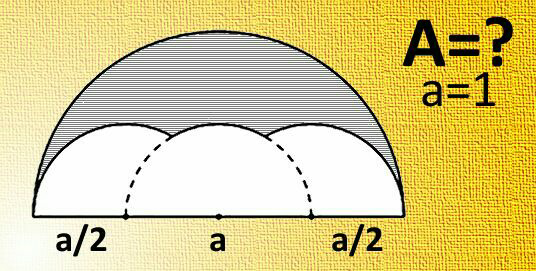
Question Number 67615 by TawaTawa last updated on 29/Aug/19
Commented by TawaTawa last updated on 29/Aug/19
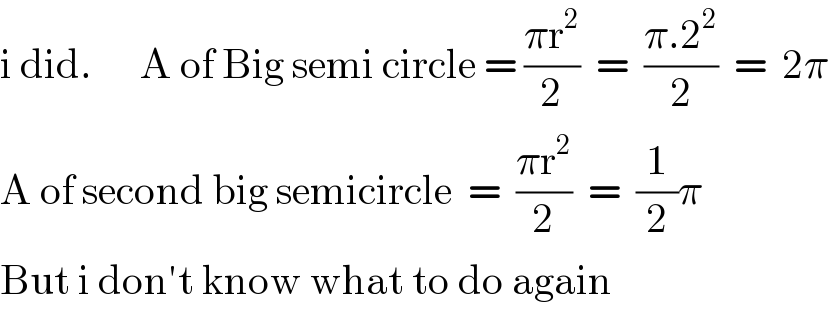
$$\mathrm{i}\:\mathrm{did}.\:\:\:\:\:\:\mathrm{A}\:\mathrm{of}\:\mathrm{Big}\:\mathrm{semi}\:\mathrm{circle}\:=\:\frac{\pi\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}\:\:=\:\:\frac{\pi.\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\:\:=\:\:\mathrm{2}\pi \\ $$$$\mathrm{A}\:\mathrm{of}\:\mathrm{second}\:\mathrm{big}\:\mathrm{semicircle}\:\:=\:\:\frac{\pi\mathrm{r}^{\mathrm{2}} }{\mathrm{2}}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\pi \\ $$$$\mathrm{But}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{what}\:\mathrm{to}\:\mathrm{do}\:\mathrm{again} \\ $$
Answered by mr W last updated on 29/Aug/19
Commented by mr W last updated on 29/Aug/19

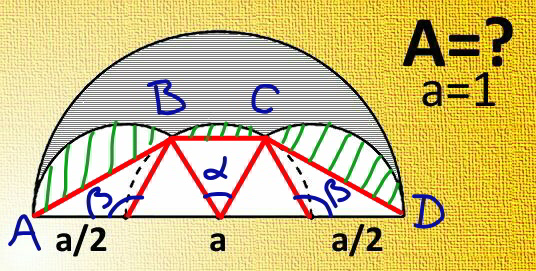
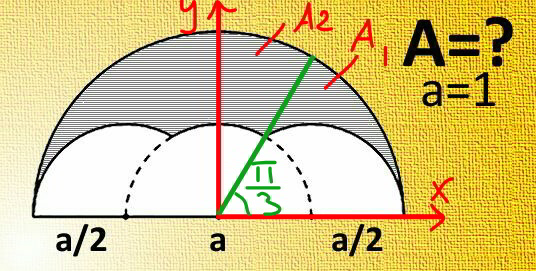
$${radius}\:{of}\:{big}\:{semi}\:{circle}={R}={a} \\ $$$${radius}\:{of}\:{small}\:{circles}={r}=\frac{{a}}{\mathrm{2}} \\ $$$$\alpha=\frac{\pi}{\mathrm{3}} \\ $$$$\beta=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${AD}=\mathrm{2}{R}=\mathrm{2}{a} \\ $$$${BC}={r}=\frac{{a}}{\mathrm{2}} \\ $$$${A}_{{ABCD}} =\frac{\frac{{a}}{\mathrm{2}}+\mathrm{2}{a}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{5}\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{16}} \\ $$$${A}_{\overset{\frown} {{AB}}} ={A}_{\overset{\frown} {{CD}}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\beta−\mathrm{sin}\:\beta\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${A}_{\overset{\frown} {{BC}}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${A}_{{shade}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−{A}_{{ABCD}} −\mathrm{2}×{A}_{\overset{\frown} {{AB}}} −{A}_{\overset{\frown} {{BC}}} \\ $$$$=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{16}}−\mathrm{2}×\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left(\frac{\mathrm{7}\pi}{\mathrm{3}}−\sqrt{\mathrm{3}}\right) \\ $$$$=\frac{{a}^{\mathrm{2}} \left(\mathrm{7}\pi−\mathrm{3}\sqrt{\mathrm{3}}\right)}{\mathrm{24}} \\ $$
Commented by TawaTawa last updated on 29/Aug/19
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 29/Aug/19
Commented by mr W last updated on 29/Aug/19
![A_1 =∫_0 ^(π/3) (1/2)(a^2 −a^2 cos^2 θ)dθ =(a^2 /2)∫_0 ^(π/3) sin^2 θdθ =(a^2 /4)∫_0 ^(π/3) (1−cos 2θ)dθ =(a^2 /4)[θ−((sin 2θ)/2)]_0 ^(π/3) =(a^2 /4)((π/3)−((√3)/4)) A_2 =(1/2)×(π/6)×(a^2 −(a^2 /4))=((a^2 π)/(16)) A_(shaded) =2(A_1 +A_2 ) =(a^2 /2)((π/3)−((√3)/4))+((πa^2 )/8) =((a^2 (7π−3(√3)))/(24))](Q67634.png)
$${A}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\right){d}\theta \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{sin}^{\mathrm{2}} \:\theta{d}\theta \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left[\theta−\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{6}}×\left({a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)=\frac{{a}^{\mathrm{2}} \pi}{\mathrm{16}} \\ $$$$ \\ $$$${A}_{{shaded}} =\mathrm{2}\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} \right) \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)+\frac{\pi{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=\frac{{a}^{\mathrm{2}} \left(\mathrm{7}\pi−\mathrm{3}\sqrt{\mathrm{3}}\right)}{\mathrm{24}} \\ $$
Commented by TawaTawa last updated on 29/Aug/19
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
