
Question Number 67531 by mathmax by abdo last updated on 28/Aug/19
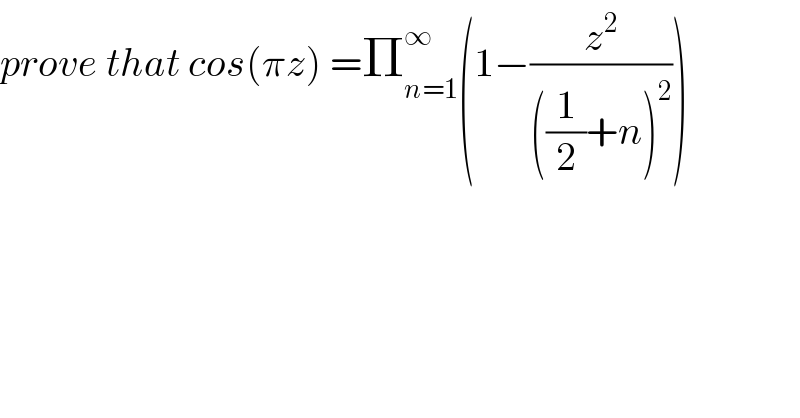
$${prove}\:{that}\:{cos}\left(\pi{z}\right)\:=\prod_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\left(\frac{\mathrm{1}}{\mathrm{2}}+{n}\right)^{\mathrm{2}} }\right) \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19
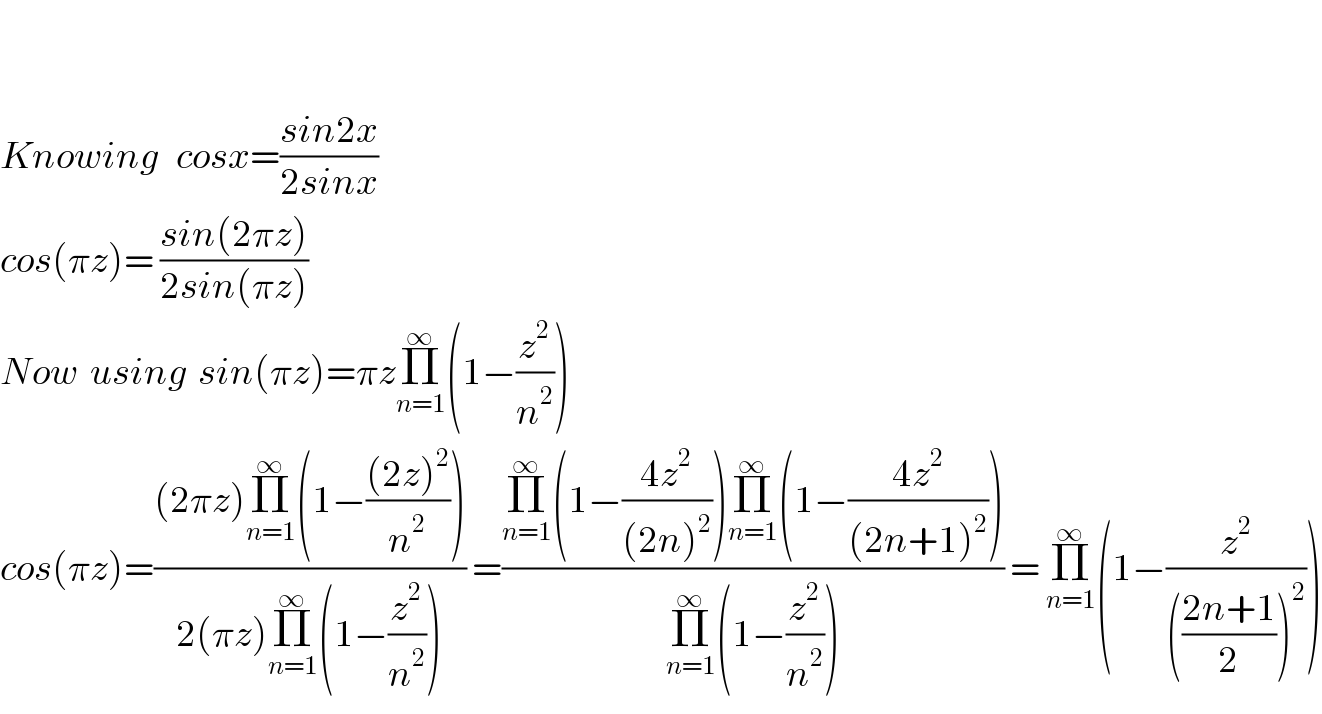
$$ \\ $$$$ \\ $$$${Knowing}\:\:\:{cosx}=\frac{{sin}\mathrm{2}{x}}{\mathrm{2}{sinx}}\: \\ $$$${cos}\left(\pi{z}\right)=\:\frac{{sin}\left(\mathrm{2}\pi{z}\right)}{\mathrm{2}{sin}\left(\pi{z}\right)}\: \\ $$$${Now}\:\:{using}\:\:{sin}\left(\pi{z}\right)=\pi{z}\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$${cos}\left(\pi{z}\right)=\frac{\left(\mathrm{2}\pi{z}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\left(\mathrm{2}{z}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)}{\mathrm{2}\left(\pi{z}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)}\:=\frac{\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{4}{z}^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{4}{z}^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)}{\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$
