
Question Number 67528 by mathmax by abdo last updated on 28/Aug/19
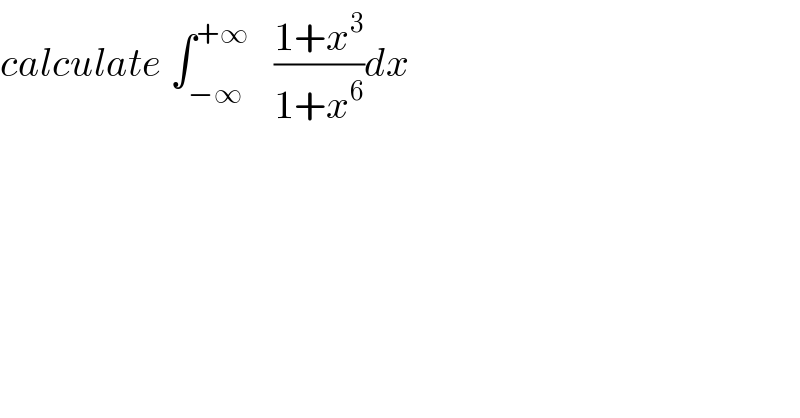
$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19

$${let}\:{named}\:{it}\:{K} \\ $$$${when}\:{changing}\:\:\:{x}=−{u}\:\:\:\:\:\: \\ $$$${K}=\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{1}−{u}^{\mathrm{3}} }{\mathrm{1}+{u}^{\mathrm{6}} }\:{du}\: \\ $$$${So}\:\:\mathrm{2}{K}=\int_{−\infty} ^{\infty} \frac{\:\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{6}} }\:\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{6}} }\:\:\:\: \\ $$$${change}\:\:{u}={v}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\:\:\Rightarrow\:{du}\:=\:\frac{{v}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{6}}{dv}\: \\ $$$${K}=\frac{\mathrm{2}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{\:\:{v}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+{v}}\:{dv}=\frac{\pi}{\mathrm{3}{sin}\left(\frac{\pi}{\mathrm{6}}\right)}=\frac{\mathrm{2}\pi}{\mathrm{3}}\: \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19

$${thank}\:{you}\:{sir}. \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19
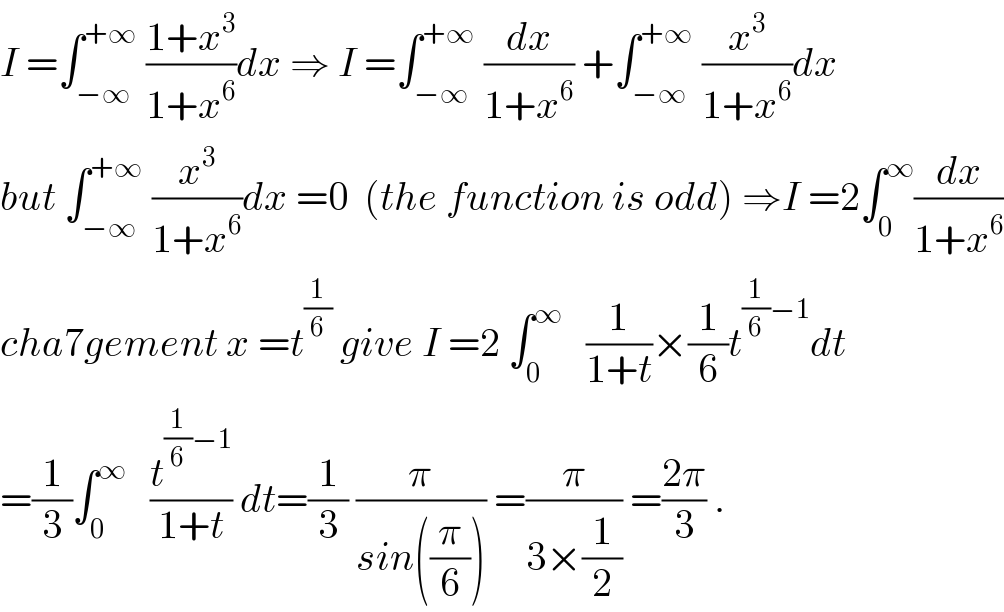
$${I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:\Rightarrow\:{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }\:+\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx} \\ $$$${but}\:\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:=\mathrm{0}\:\:\left({the}\:{function}\:{is}\:{odd}\right)\:\Rightarrow{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} } \\ $$$${cha}\mathrm{7}{gement}\:{x}\:={t}^{\frac{\mathrm{1}}{\mathrm{6}}} \:{give}\:{I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}}×\frac{\mathrm{1}}{\mathrm{6}}{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt}=\frac{\mathrm{1}}{\mathrm{3}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{6}}\right)}\:=\frac{\pi}{\mathrm{3}×\frac{\mathrm{1}}{\mathrm{2}}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}}\:. \\ $$
