
Previous in Relation and Functions Next in Relation and Functions
Question Number 67519 by mathmax by abdo last updated on 28/Aug/19
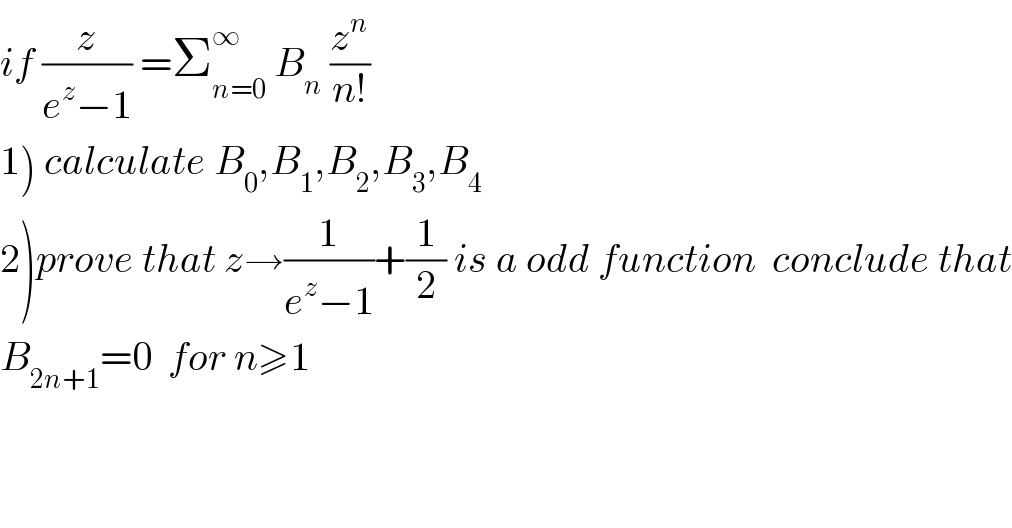
$${if}\:\frac{{z}}{{e}^{{z}} −\mathrm{1}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{B}_{{n}} \:\frac{{z}^{{n}} }{{n}!} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{B}_{\mathrm{0}} ,{B}_{\mathrm{1}} ,{B}_{\mathrm{2}} ,{B}_{\mathrm{3}} ,{B}_{\mathrm{4}} \\ $$$$\left.\mathrm{2}\right){prove}\:{that}\:{z}\rightarrow\frac{\mathrm{1}}{{e}^{{z}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\:{is}\:{a}\:{odd}\:{function}\:\:{conclude}\:{that} \\ $$$${B}_{\mathrm{2}{n}+\mathrm{1}} =\mathrm{0}\:\:{for}\:{n}\geqslant\mathrm{1} \\ $$
