
Question Number 67517 by mathmax by abdo last updated on 28/Aug/19
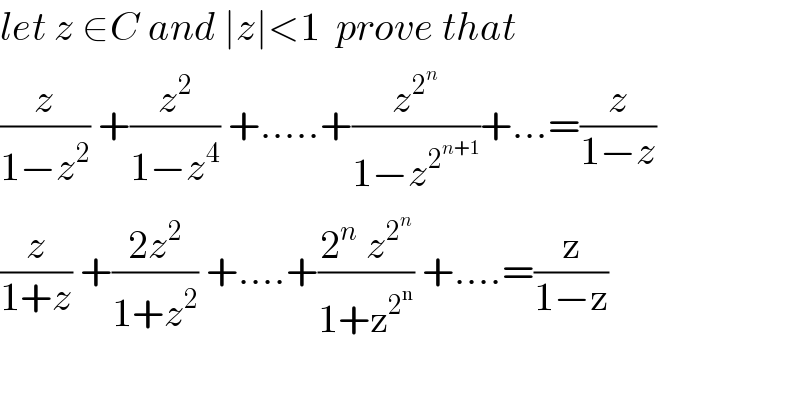
$${let}\:{z}\:\in{C}\:{and}\:\mid{z}\mid<\mathrm{1}\:\:{prove}\:{that} \\ $$ $$\frac{{z}}{\mathrm{1}−{z}^{\mathrm{2}} }\:+\frac{{z}^{\mathrm{2}} }{\mathrm{1}−{z}^{\mathrm{4}} }\:+.....+\frac{{z}^{\mathrm{2}^{{n}} } }{\mathrm{1}−{z}^{\mathrm{2}^{{n}+\mathrm{1}} } }+...=\frac{{z}}{\mathrm{1}−{z}} \\ $$ $$\frac{{z}}{\mathrm{1}+{z}}\:+\frac{\mathrm{2}{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }\:+....+\frac{\mathrm{2}^{{n}} \:{z}^{\mathrm{2}^{{n}} } }{\mathrm{1}+\mathrm{z}^{\mathrm{2}^{\mathrm{n}} } }\:+....=\frac{\mathrm{z}}{\mathrm{1}−\mathrm{z}} \\ $$
