
Question Number 67393 by Prof 40 last updated on 26/Aug/19
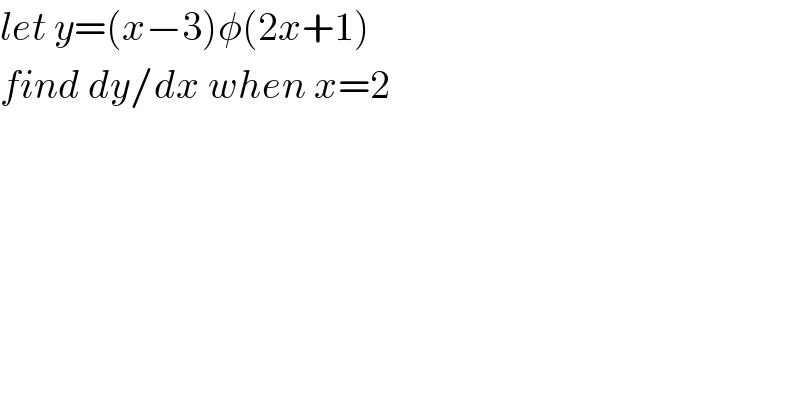
$${let}\:{y}=\left({x}−\mathrm{3}\right)\phi\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$${find}\:{dy}/{dx}\:{when}\:{x}=\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19
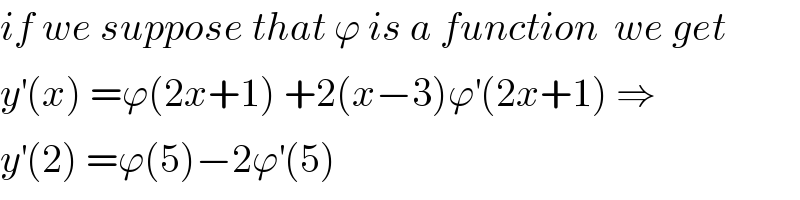
$${if}\:{we}\:{suppose}\:{that}\:\varphi\:{is}\:{a}\:{function}\:\:{we}\:{get} \\ $$$${y}^{'} \left({x}\right)\:=\varphi\left(\mathrm{2}{x}+\mathrm{1}\right)\:+\mathrm{2}\left({x}−\mathrm{3}\right)\varphi^{'} \left(\mathrm{2}{x}+\mathrm{1}\right)\:\Rightarrow \\ $$$${y}^{'} \left(\mathrm{2}\right)\:=\varphi\left(\mathrm{5}\right)−\mathrm{2}\varphi^{'} \left(\mathrm{5}\right) \\ $$
