
Question Number 67337 by ajfour last updated on 25/Aug/19
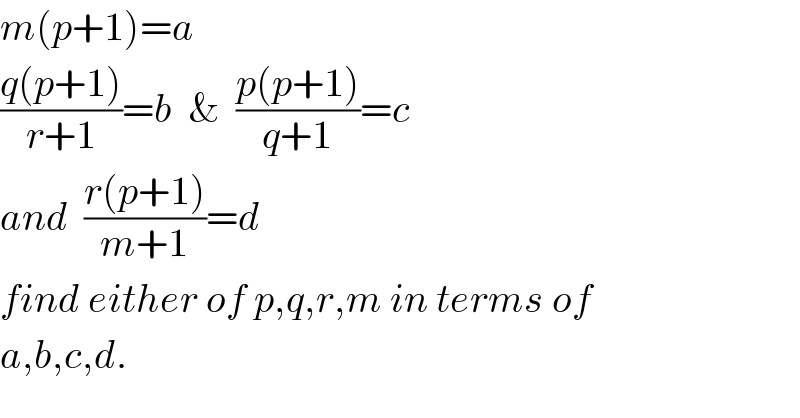
$${m}\left({p}+\mathrm{1}\right)={a} \\ $$ $$\frac{{q}\left({p}+\mathrm{1}\right)}{{r}+\mathrm{1}}={b}\:\:\&\:\:\frac{{p}\left({p}+\mathrm{1}\right)}{{q}+\mathrm{1}}={c} \\ $$ $${and}\:\:\frac{{r}\left({p}+\mathrm{1}\right)}{{m}+\mathrm{1}}={d} \\ $$ $${find}\:{either}\:{of}\:{p},{q},{r},{m}\:{in}\:{terms}\:{of} \\ $$ $${a},{b},{c},{d}. \\ $$
Answered by mr W last updated on 25/Aug/19
/b)−1 r(p+1)=d(m+1) {[((p(p+1))/c)−1]((p+1)/b)−1}(p+1)=((a/(p+1))+1)d let p+1=t {[(t−1)t−c]t−bc}t^2 =(a+t)bcd ⇒t^5 −t^4 −ct^3 −bct^2 −bcdt−abcd=0 ......???](Q67340.png)
$${m}=\frac{{a}}{{p}+\mathrm{1}} \\ $$ $${q}=\frac{{p}\left({p}+\mathrm{1}\right)}{{c}}−\mathrm{1} \\ $$ $${r}=\frac{{q}\left({p}+\mathrm{1}\right)}{{b}}−\mathrm{1}=\left[\frac{{p}\left({p}+\mathrm{1}\right)}{{c}}−\mathrm{1}\right]\frac{{p}+\mathrm{1}}{{b}}−\mathrm{1} \\ $$ $${r}\left({p}+\mathrm{1}\right)={d}\left({m}+\mathrm{1}\right) \\ $$ $$\left\{\left[\frac{{p}\left({p}+\mathrm{1}\right)}{{c}}−\mathrm{1}\right]\frac{{p}+\mathrm{1}}{{b}}−\mathrm{1}\right\}\left({p}+\mathrm{1}\right)=\left(\frac{{a}}{{p}+\mathrm{1}}+\mathrm{1}\right){d} \\ $$ $${let}\:{p}+\mathrm{1}={t} \\ $$ $$\left\{\left[\left({t}−\mathrm{1}\right){t}−{c}\right]{t}−{bc}\right\}{t}^{\mathrm{2}} =\left({a}+{t}\right){bcd} \\ $$ $$\Rightarrow{t}^{\mathrm{5}} −{t}^{\mathrm{4}} −{ct}^{\mathrm{3}} −{bct}^{\mathrm{2}} −{bcdt}−{abcd}=\mathrm{0} \\ $$ $$......??? \\ $$
Commented byajfour last updated on 26/Aug/19

$${trying}\:{again}\:{to}\:{solve}\:{the}\:{general} \\ $$ $${quintic}\:{i}\:{have}\:{stuck}\:{upon}\:{this}\:{Sir}! \\ $$
