
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 67281 by Tony Lin last updated on 25/Aug/19
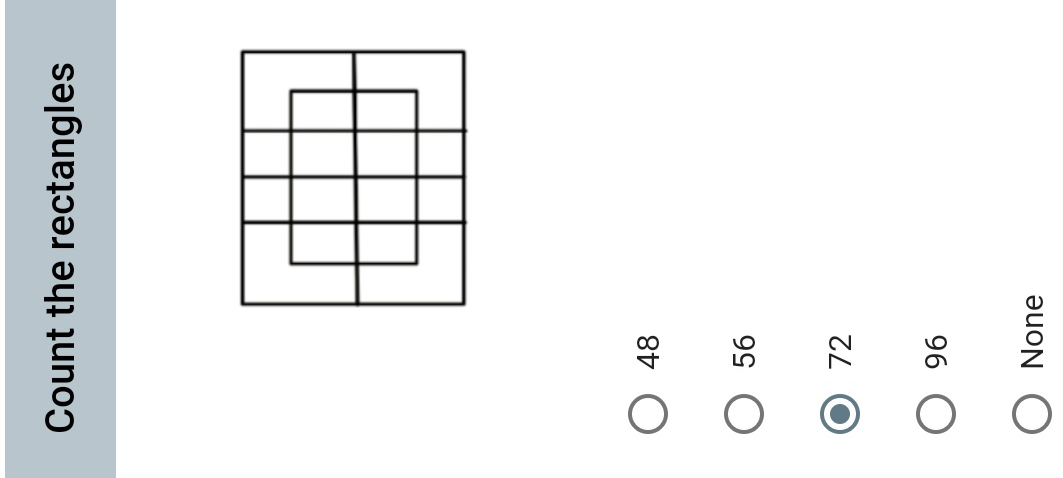
Commented by mr W last updated on 25/Aug/19
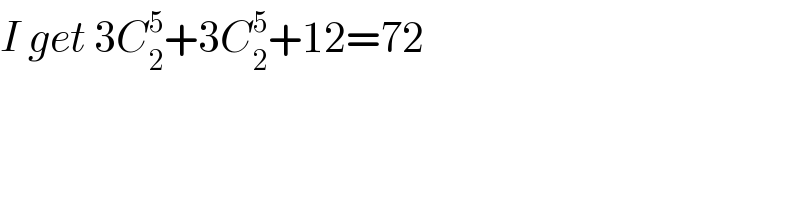
$${I}\:{get}\:\mathrm{3}{C}_{\mathrm{2}} ^{\mathrm{5}} +\mathrm{3}{C}_{\mathrm{2}} ^{\mathrm{5}} +\mathrm{12}=\mathrm{72} \\ $$
Commented by Tony Lin last updated on 25/Aug/19

$${Repost}\:{Question}\:{No}.\mathrm{66681} \\ $$
Commented by Tony Lin last updated on 25/Aug/19
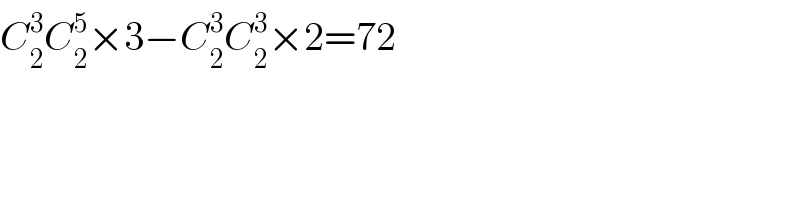
$${C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{3}−{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{3}} ×\mathrm{2}=\mathrm{72} \\ $$
Commented by Tony Lin last updated on 25/Aug/19
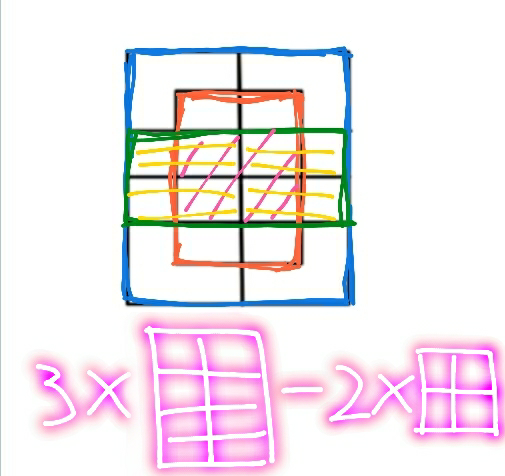
Commented by Tony Lin last updated on 25/Aug/19

$${orange}\:{part}\left(\mathrm{2}×\mathrm{4}\:{inside}\right) \\ $$$$\Rightarrow{choose}\:{two}\:{from}\:{three}\:{vertical}\:{lines} \\ $$$$\Rightarrow{choose}\:{two}\:{from}\:{five}\:{horizontal}\:{lines} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{30} \\ $$$${blue}\:{part}\left(\mathrm{2}×\mathrm{4}\:{outside}\right) \\ $$$$\Rightarrow{the}\:{same}\:{as}\:{the}\:{orange}\:{part} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{30} \\ $$$${green}\:{part}\left(\mathrm{2}×\mathrm{4}\:{middle}\right) \\ $$$$\Rightarrow{only}\:{in}\:{this}\:{part}\:{the}\:{rectangles}\:{outside} \\ $$$${combine}\:{with}\:\:{the}\:{rectangles}\:{inside}\: \\ $$$$\Rightarrow{the}\:{same}\:{as}\:{the}\:{orange}\:{part} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{30} \\ $$$${pink}\:{part}\left(\mathrm{2}×\mathrm{2}\:{inside}\right) \\ $$$$\Rightarrow{we}\:{have}\:{already}\:{counted}\:{this}\:{part} \\ $$$${in}\:{the}\:{orange}\:{part}\:{but}\:{we}\:{count}\:{this}\: \\ $$$${part}\:{again}\:{in}\:{the}\:{green}\:{part} \\ $$$$\Rightarrow{choose}\:{two}\:{from}\:{three}\:{vertical}\:{lines} \\ $$$$\Rightarrow{choose}\:{two}\:{from}\:{three}\:{horizontal}\:{lines} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{9} \\ $$$${yellow}\:{part}\left(\mathrm{2}×\mathrm{2}\:{outside}\right) \\ $$$$\Rightarrow{we}\:{have}\:{already}\:{counted}\:{this}\:{part} \\ $$$${in}\:{the}\:{blue}\:{part}\:{but}\:{we}\:{count}\:{this} \\ $$$${part}\:{again}\:{in}\:{the}\:{green}\:{part} \\ $$$$\Rightarrow{the}\:{same}\:{as}\:{the}\:{pink}\:{part} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{9} \\ $$$$\therefore{there}\:{are}\:\left({C}_{\mathrm{2}} ^{\mathrm{5}} {C}_{\mathrm{2}} ^{\mathrm{3}} ×\mathrm{3}−{C}_{\mathrm{2}} ^{\mathrm{3}} {C}_{\mathrm{2}} ^{\mathrm{3}} ×\mathrm{2}=\mathrm{72}\right)\:{rectangles} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Aug/19

$$\mathrm{Sir}\:\mathrm{Tony}\:\mathrm{Lin},\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:\mathrm{any}\:\mathrm{error}\:\mathrm{in} \\ $$$$\mathrm{your}\:\mathrm{approach}.\mathrm{However}\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{where}'\mathrm{s}\:\mathrm{deffect}\:\mathrm{in}\:\mathrm{my}\:\mathrm{approach}!\:\mathrm{Pl} \\ $$$$\mathrm{cooperate}\:\mathrm{with}\:\mathrm{me}. \\ $$
Answered by Rasheed.Sindhi last updated on 25/Aug/19
Commented by Rasheed.Sindhi last updated on 25/Aug/19

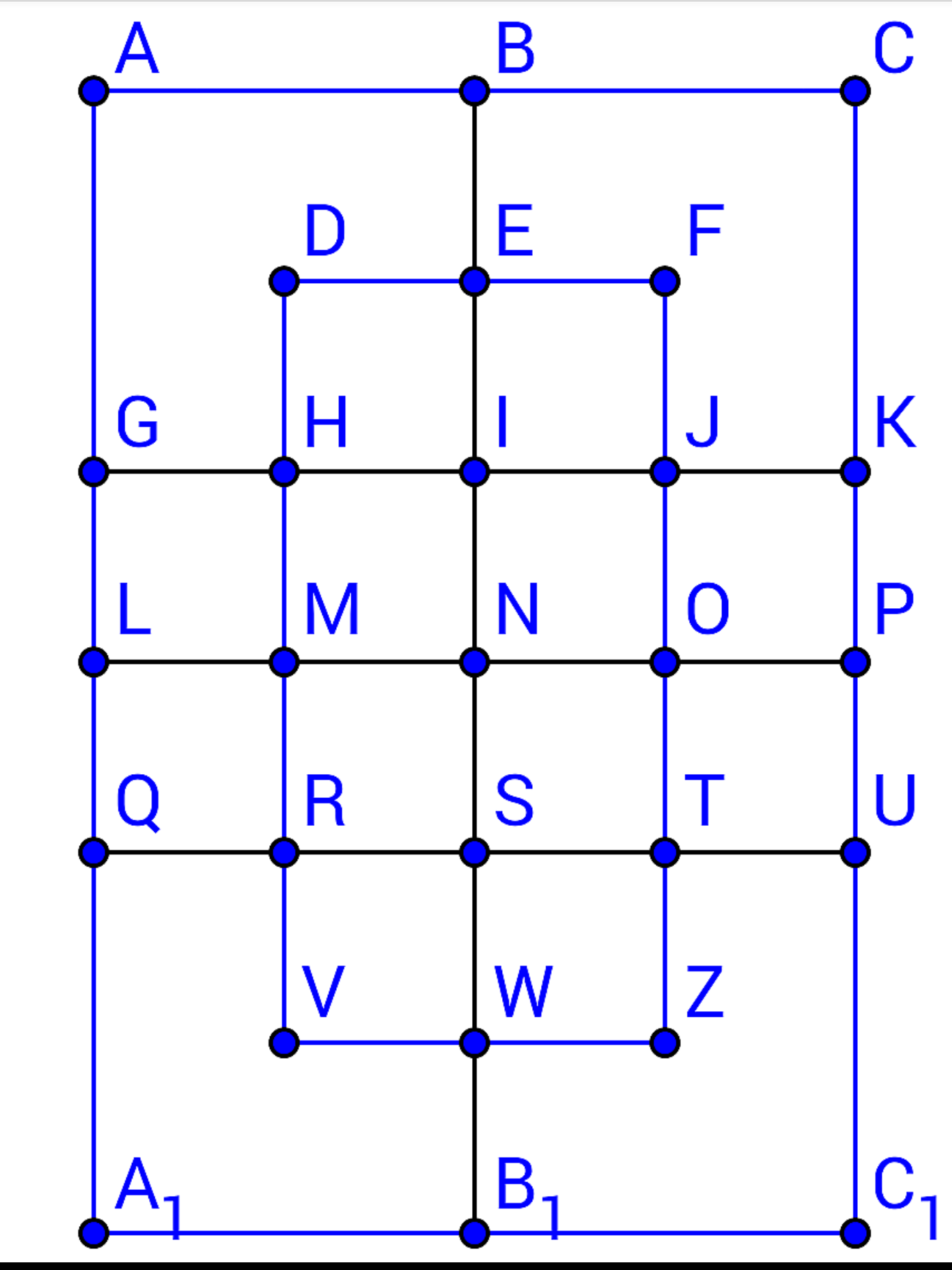
$$\:^{\bullet} {In}\:{order}\:{to}\:{prevent}\:{missing}/{repeating} \\ $$$${in}\:{counting},{we}'{ll}\:{count}\:{rectangles}\:{with} \\ $$$${their}\:\boldsymbol{{left}}-\boldsymbol{{upper}}\:\boldsymbol{{corners}}.{For}\:{example} \\ $$$${all}\:{the}\:{rectangles}\:{whose}\:{left}-{upper} \\ $$$${corner}\:{is}\:\mathrm{A}\:{will}\:{be}\:{counted}\:{together} \\ $$$${and}\:{recorded}\:{with}\:\mathrm{A}.{In}\:{this}\:{way}\:{we} \\ $$$${will}\:{count}\:{rectangles}\:{with}\:{each}\:{and} \\ $$$${every}\:{vertex}. \\ $$$$\:^{\bullet} \mathrm{A}:\:\mathcal{E}{dges}\:{from}\:\mathrm{A}\:{to}\:{the}\:{left}: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{AB},\mathrm{AC}\:\left(\mathrm{2}\:{edges}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathcal{E}{dges}\:{from}\:\mathrm{A}\:{to}\:{the}\:{down}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{AG},\mathrm{AL},\mathrm{AQ},\mathrm{AA}_{\mathrm{1}} \:\left(\mathrm{4}\:{edges}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore{Number}\:{of}\:{rectangles}\:{with}\:{left}- \\ $$$$\:\:\:\:\:\:\:\:\:{upper}\:{corner}\:\mathrm{A}=\mathrm{2}×\mathrm{4}=\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\left({Recall}\:{that}\:{every}\:{upper}\:{edge}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:{makes}\:{a}\:{rectangle}\:{with}\:{every} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:{left}\:{edge}.\right) \\ $$$$\:\:\:\:\:\:\:\:\:....... \\ $$
Commented by Tony Lin last updated on 25/Aug/19
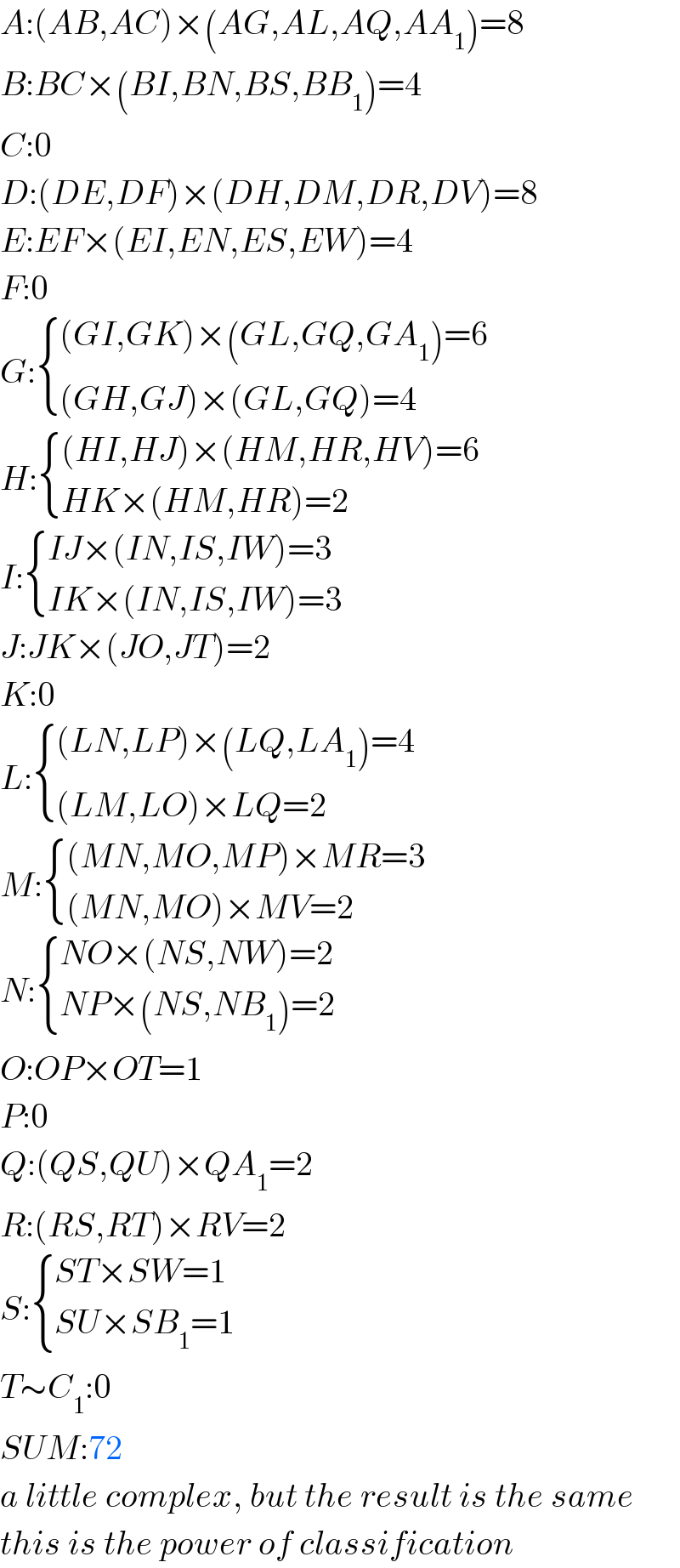
$${A}:\left({AB},{AC}\right)×\left({AG},{AL},{AQ},{AA}_{\mathrm{1}} \right)=\mathrm{8} \\ $$$${B}:{BC}×\left({BI},{BN},{BS},{BB}_{\mathrm{1}} \right)=\mathrm{4} \\ $$$${C}:\mathrm{0} \\ $$$${D}:\left({DE},{DF}\right)×\left({DH},{DM},{DR},{DV}\right)=\mathrm{8} \\ $$$${E}:{EF}×\left({EI},{EN},{ES},{EW}\right)=\mathrm{4} \\ $$$${F}:\mathrm{0} \\ $$$${G}:\begin{cases}{\left({GI},{GK}\right)×\left({GL},{GQ},{GA}_{\mathrm{1}} \right)=\mathrm{6}}\\{\left({GH},{GJ}\right)×\left({GL},{GQ}\right)=\mathrm{4}}\end{cases} \\ $$$${H}:\begin{cases}{\left({HI},{HJ}\right)×\left({HM},{HR},{HV}\right)=\mathrm{6}}\\{{HK}×\left({HM},{HR}\right)=\mathrm{2}}\end{cases} \\ $$$${I}:\begin{cases}{{IJ}×\left({IN},{IS},{IW}\right)=\mathrm{3}}\\{{IK}×\left({IN},{IS},{IW}\right)=\mathrm{3}}\end{cases} \\ $$$${J}:{JK}×\left({JO},{JT}\right)=\mathrm{2} \\ $$$${K}:\mathrm{0} \\ $$$${L}:\begin{cases}{\left({LN},{LP}\right)×\left({LQ},{LA}_{\mathrm{1}} \right)=\mathrm{4}}\\{\left({LM},{LO}\right)×{LQ}=\mathrm{2}}\end{cases} \\ $$$${M}:\begin{cases}{\left({MN},{MO},{MP}\right)×{MR}=\mathrm{3}}\\{\left({MN},{MO}\right)×{MV}=\mathrm{2}}\end{cases} \\ $$$${N}:\begin{cases}{{NO}×\left({NS},{NW}\right)=\mathrm{2}}\\{{NP}×\left({NS},{NB}_{\mathrm{1}} \right)=\mathrm{2}}\end{cases} \\ $$$${O}:{OP}×{OT}=\mathrm{1} \\ $$$${P}:\mathrm{0} \\ $$$${Q}:\left({QS},{QU}\right)×{QA}_{\mathrm{1}} =\mathrm{2} \\ $$$${R}:\left({RS},{RT}\right)×{RV}=\mathrm{2} \\ $$$${S}:\begin{cases}{{ST}×{SW}=\mathrm{1}}\\{{SU}×{SB}_{\mathrm{1}} =\mathrm{1}}\end{cases} \\ $$$${T}\sim{C}_{\mathrm{1}} :\mathrm{0} \\ $$$${SUM}:\mathrm{72} \\ $$$${a}\:{little}\:{complex},\:{but}\:{the}\:{result}\:{is}\:{the}\:{same} \\ $$$${this}\:{is}\:{the}\:{power}\:{of}\:{classification} \\ $$
Commented by peter frank last updated on 25/Aug/19
$${thank}\:{you}\:{both} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Aug/19

$$\mathcal{G}{reat}\:\mathcal{T}{hanks}\:{for}\:\mathcal{G}{reat}\:\mathcal{H}{elp}\:\mathrm{S}\overset{\blacklozenge} {\parallel}\mathrm{R}! \\ $$$$\mathcal{I}\:{found}\:{my}\:{mistake}\:{after}\:{comparing} \\ $$$${my}\:{work}\:{with}\:{yours}! \\ $$$$ \\ $$$${Also}\:{thank}\:\Cup\:{Peter}\:{Frank}! \\ $$
