
Question Number 6687 by Tawakalitu. last updated on 13/Jul/16
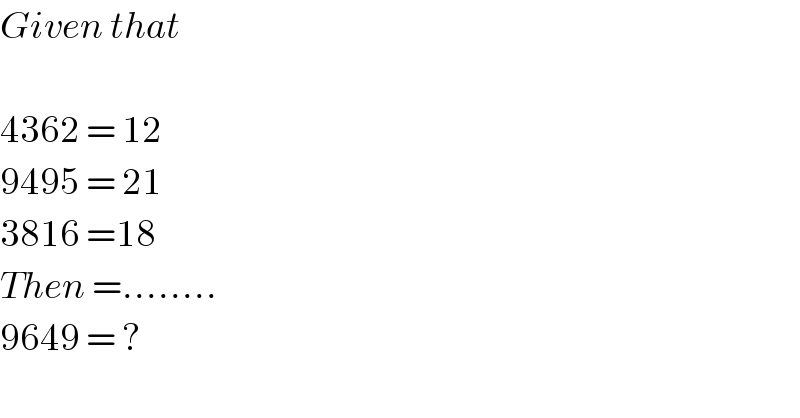
$${Given}\:{that} \\ $$$$ \\ $$$$\mathrm{4362}\:=\:\mathrm{12} \\ $$$$\mathrm{9495}\:=\:\mathrm{21} \\ $$$$\mathrm{3816}\:=\mathrm{18} \\ $$$${Then}\:=........ \\ $$$$\mathrm{9649}\:=\:? \\ $$
Answered by Rasheed Soomro last updated on 14/Jul/16
![4362 = 12 9495 = 21 3816 =18 9649 = ? −−−−−−−−−−−−−−−−−−−−− I have discovered one logic. Other logics may be possible. I am writing my logic in a form of formula here. (Sum of digits)−[ (unit digit+1)(mod 7) ] (4+3+6+2)−[(2+1)(mod 7)]=15−3=12 (9+4+9+5)−[(5+1)(mod 7)]=27−6=21 (3+8+1+6)−[(6+1)(mod 7)]=18−0=18 So, (9+6+4+9)−[(9+1)(mod 7)]=28−3=∥25∥_(=) ^(=)](Q6697.png)
$$\mathrm{4362}\:=\:\mathrm{12} \\ $$$$\mathrm{9495}\:=\:\mathrm{21} \\ $$$$\mathrm{3816}\:=\mathrm{18} \\ $$$$\mathrm{9649}\:=\:? \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$${I}\:{have}\:{discovered}\:{one}\:{logic}.\:{Other}\:{logics} \\ $$$${may}\:{be}\:{possible}.\:{I}\:{am}\:{writing}\:{my}\:{logic} \\ $$$${in}\:{a}\:{form}\:{of}\:{formula}\:{here}. \\ $$$$\:\:\:\:\:\:\:\:\:\left(\boldsymbol{{Sum}}\:\boldsymbol{{of}}\:\boldsymbol{{digits}}\right)−\left[\:\left(\boldsymbol{{unit}}\:\boldsymbol{{digit}}+\mathrm{1}\right)\left(\boldsymbol{{mod}}\:\mathrm{7}\right)\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{4}+\mathrm{3}+\mathrm{6}+\mathrm{2}\right)−\left[\left(\mathrm{2}+\mathrm{1}\right)\left({mod}\:\mathrm{7}\right)\right]=\mathrm{15}−\mathrm{3}=\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{9}+\mathrm{4}+\mathrm{9}+\mathrm{5}\right)−\left[\left(\mathrm{5}+\mathrm{1}\right)\left({mod}\:\mathrm{7}\right)\right]=\mathrm{27}−\mathrm{6}=\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}+\mathrm{8}+\mathrm{1}+\mathrm{6}\right)−\left[\left(\mathrm{6}+\mathrm{1}\right)\left({mod}\:\mathrm{7}\right)\right]=\mathrm{18}−\mathrm{0}=\mathrm{18} \\ $$$${So}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{9}+\mathrm{6}+\mathrm{4}+\mathrm{9}\right)−\left[\left(\mathrm{9}+\mathrm{1}\right)\left({mod}\:\mathrm{7}\right)\right]=\mathrm{28}−\mathrm{3}=\underset{=} {\overset{=} {\parallel\mathrm{25}\parallel}} \\ $$
Commented by Tawakalitu. last updated on 15/Jul/16

$${Wow}\:{thanks}. \\ $$
