Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 66546 by Sayantan chakraborty last updated on 17/Aug/19

Commented by Sayantan chakraborty last updated on 17/Aug/19

urgent need

$$\mathrm{urgent}\:\mathrm{need} \\ $$

Commented by ~ À ® @ 237 ~ last updated on 17/Aug/19

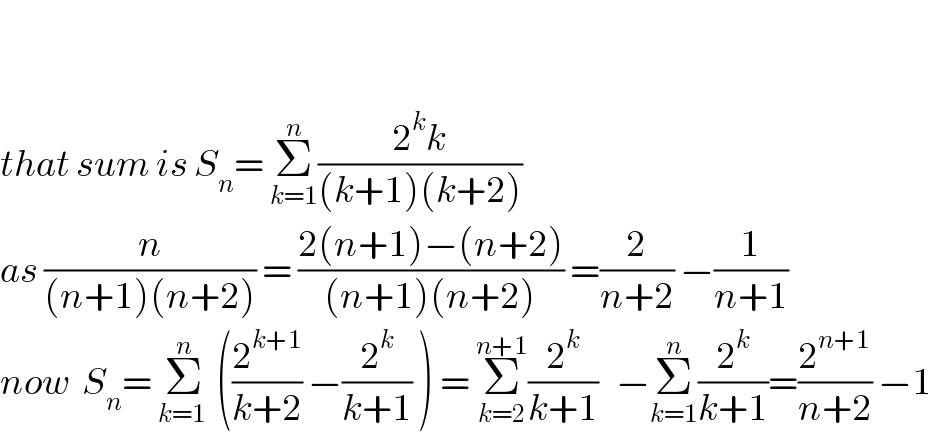
that sum is S_n = Σ_(k=1) ^n ((2^k k)/((k+1)(k+2))) as (n/((n+1)(n+2))) = ((2(n+1)−(n+2))/((n+1)(n+2))) =(2/(n+2)) −(1/(n+1)) now S_n = Σ_(k=1 ) ^n ((2^(k+1) /(k+2)) −(2^k /(k+1)) ) = Σ_(k=2) ^(n+1) (2^k /(k+1)) −Σ_(k=1) ^n (2^k /(k+1))=(2^(n+1) /(n+2)) −1

$$ \\ $$$$ \\ $$$${that}\:{sum}\:{is}\:{S}_{{n}} =\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} {k}}{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}\: \\ $$$${as}\:\frac{{n}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:=\:\frac{\mathrm{2}\left({n}+\mathrm{1}\right)−\left({n}+\mathrm{2}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:=\frac{\mathrm{2}}{{n}+\mathrm{2}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\: \\ $$$${now}\:\:{S}_{{n}} =\:\underset{{k}=\mathrm{1}\:} {\overset{{n}} {\sum}}\:\left(\frac{\mathrm{2}^{{k}+\mathrm{1}} }{{k}+\mathrm{2}}\:−\frac{\mathrm{2}^{{k}} }{{k}+\mathrm{1}}\:\right)\:=\:\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\mathrm{2}^{{k}} }{{k}+\mathrm{1}}\:\:\:−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} }{{k}+\mathrm{1}}=\frac{\mathrm{2}^{{n}+\mathrm{1}} }{{n}+\mathrm{2}}\:−\mathrm{1} \\ $$

Commented by Cmr 237 last updated on 17/Aug/19

please i need explication at the end of your demonstration please

$${please}\:{i}\:{need}\:{explication}\:{at}\:{the}\:{end}\:{of}\:\:{your}\:{demonstration}\:{please} \\ $$

Commented by Sayantan chakraborty last updated on 17/Aug/19

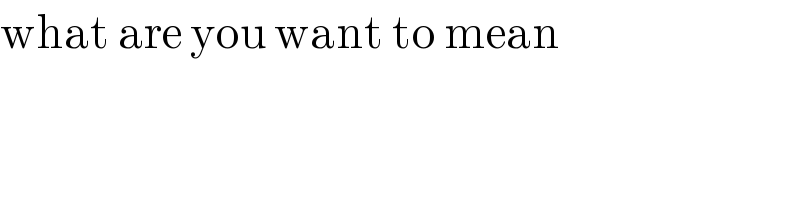
what are you want to mean

$$\mathrm{what}\:\mathrm{are}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{mean} \\ $$

Commented by Cmr 237 last updated on 17/Aug/19

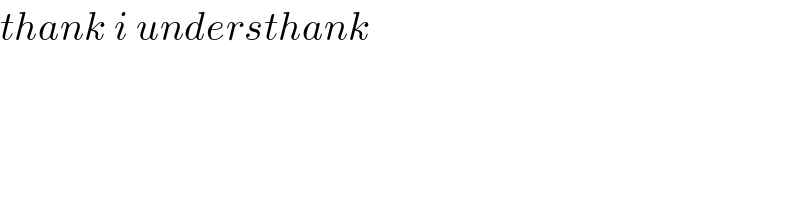
thank i understhank

$${thank}\:{i}\:{understhank} \\ $$

Commented by mathmax by abdo last updated on 17/Aug/19

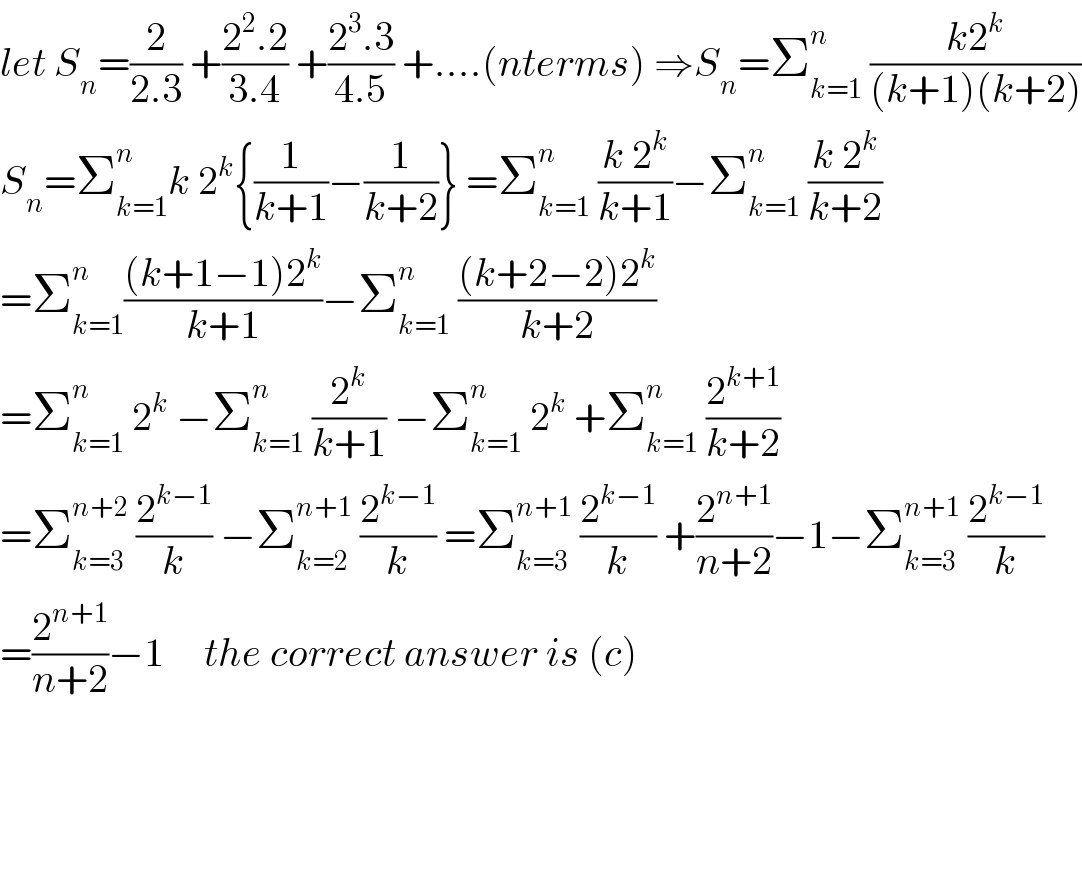
let S_n =(2/(2.3)) +((2^2 .2)/(3.4)) +((2^3 .3)/(4.5)) +....(nterms) ⇒S_n =Σ_(k=1) ^n ((k2^k )/((k+1)(k+2))) S_n =Σ_(k=1) ^n k 2^k {(1/(k+1))−(1/(k+2))} =Σ_(k=1) ^n ((k 2^k )/(k+1))−Σ_(k=1) ^n ((k 2^k )/(k+2)) =Σ_(k=1) ^n (((k+1−1)2^k )/(k+1))−Σ_(k=1) ^n (((k+2−2)2^k )/(k+2)) =Σ_(k=1) ^n 2^k −Σ_(k=1) ^n (2^k /(k+1)) −Σ_(k=1) ^n 2^k +Σ_(k=1) ^n (2^(k+1) /(k+2)) =Σ_(k=3) ^(n+2) (2^(k−1) /k) −Σ_(k=2) ^(n+1) (2^(k−1) /k) =Σ_(k=3) ^(n+1) (2^(k−1) /k) +(2^(n+1) /(n+2))−1−Σ_(k=3) ^(n+1) (2^(k−1) /k) =(2^(n+1) /(n+2))−1 the correct answer is (c)

$${let}\:{S}_{{n}} =\frac{\mathrm{2}}{\mathrm{2}.\mathrm{3}}\:+\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{2}}{\mathrm{3}.\mathrm{4}}\:+\frac{\mathrm{2}^{\mathrm{3}} .\mathrm{3}}{\mathrm{4}.\mathrm{5}}\:+....\left({nterms}\right)\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}\mathrm{2}^{{k}} }{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:\mathrm{2}^{{k}} \left\{\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{{k}+\mathrm{2}}\right\}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}\:\mathrm{2}^{{k}} }{{k}+\mathrm{1}}−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}\:\mathrm{2}^{{k}} }{{k}+\mathrm{2}} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left({k}+\mathrm{1}−\mathrm{1}\right)\mathrm{2}^{{k}} }{{k}+\mathrm{1}}−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left({k}+\mathrm{2}−\mathrm{2}\right)\mathrm{2}^{{k}} }{{k}+\mathrm{2}} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\mathrm{2}^{{k}} \:−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{k}} }{{k}+\mathrm{1}}\:−\sum_{{k}=\mathrm{1}} ^{{n}} \:\mathrm{2}^{{k}} \:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{k}+\mathrm{1}} }{{k}+\mathrm{2}} \\ $$$$=\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{2}} \:\frac{\mathrm{2}^{{k}−\mathrm{1}} }{{k}}\:−\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{2}^{{k}−\mathrm{1}} }{{k}}\:=\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{2}^{{k}−\mathrm{1}} }{{k}}\:+\frac{\mathrm{2}^{{n}+\mathrm{1}} }{{n}+\mathrm{2}}−\mathrm{1}−\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{2}^{{k}−\mathrm{1}} }{{k}} \\ $$$$=\frac{\mathrm{2}^{{n}+\mathrm{1}} }{{n}+\mathrm{2}}−\mathrm{1}\:\:\:\:\:{the}\:{correct}\:{answer}\:{is}\:\left({c}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com