
Question Number 66508 by Masumsiddiqui399@gmail.com last updated on 16/Aug/19

Commented by Prithwish sen last updated on 16/Aug/19
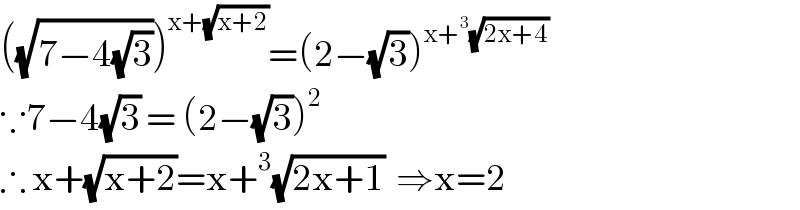
$$\left(\sqrt{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}\right)^{\mathrm{x}+\sqrt{\mathrm{x}+\mathrm{2}}} =\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{x}+^{\mathrm{3}} \sqrt{\mathrm{2x}+\mathrm{4}}} \\ $$$$\because\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\:=\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\therefore\:\mathrm{x}+\sqrt{\mathrm{x}+\mathrm{2}}=\mathrm{x}+^{\mathrm{3}} \sqrt{\mathrm{2x}+\mathrm{1}}\:\:\Rightarrow\mathrm{x}=\mathrm{2} \\ $$
Commented by MJS last updated on 16/Aug/19

$${x}=\mathrm{2}\vee{x}=−\mathrm{2} \\ $$
Commented by Prithwish sen last updated on 16/Aug/19
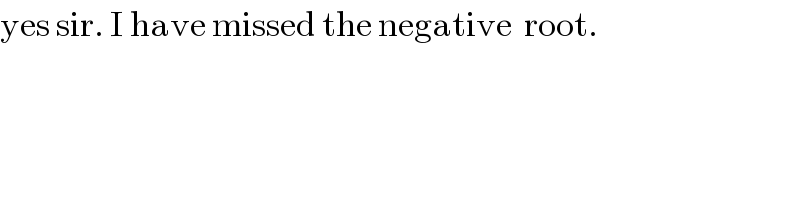
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{have}\:\mathrm{missed}\:\mathrm{the}\:\mathrm{negative}\:\:\mathrm{root}. \\ $$
