
Question Number 66126 by Joel122 last updated on 09/Aug/19
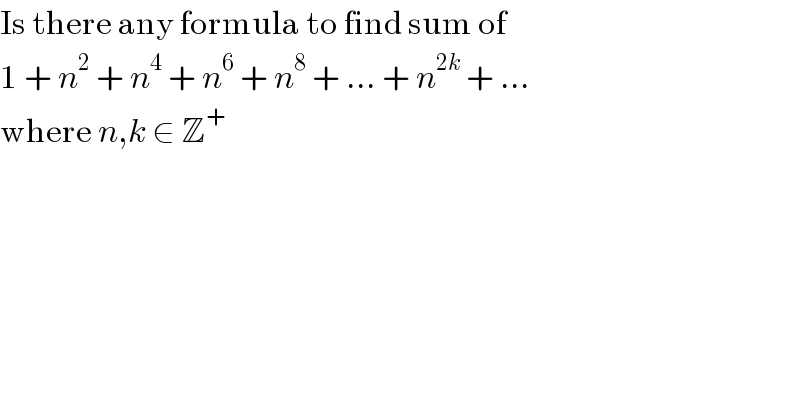
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{formula}\:\mathrm{to}\:\mathrm{find}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{1}\:+\:{n}^{\mathrm{2}} \:+\:{n}^{\mathrm{4}} \:+\:{n}^{\mathrm{6}} \:+\:{n}^{\mathrm{8}} \:+\:...\:+\:{n}^{\mathrm{2}{k}} \:+\:... \\ $$$$\mathrm{where}\:{n},{k}\:\in\:\mathbb{Z}^{+} \: \\ $$
Answered by mr W last updated on 09/Aug/19
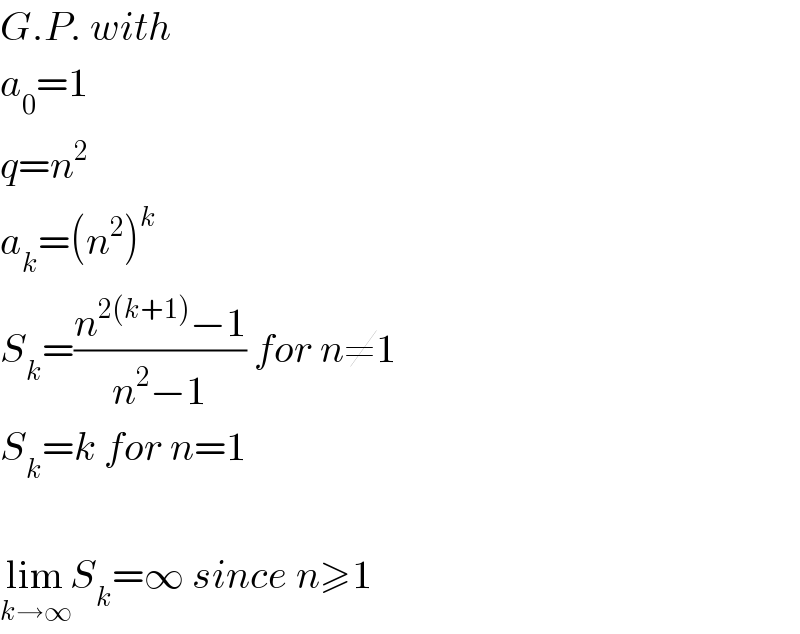
$${G}.{P}.\:{with} \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${q}={n}^{\mathrm{2}} \\ $$$${a}_{{k}} =\left({n}^{\mathrm{2}} \right)^{{k}} \\ $$$${S}_{{k}} =\frac{{n}^{\mathrm{2}\left({k}+\mathrm{1}\right)} −\mathrm{1}}{{n}^{\mathrm{2}} −\mathrm{1}}\:{for}\:{n}\neq\mathrm{1} \\ $$$${S}_{{k}} ={k}\:{for}\:{n}=\mathrm{1} \\ $$$$ \\ $$$$\underset{{k}\rightarrow\infty} {\mathrm{lim}}{S}_{{k}} =\infty\:{since}\:{n}\geqslant\mathrm{1} \\ $$
