
Question Number 66098 by aliesam last updated on 09/Aug/19
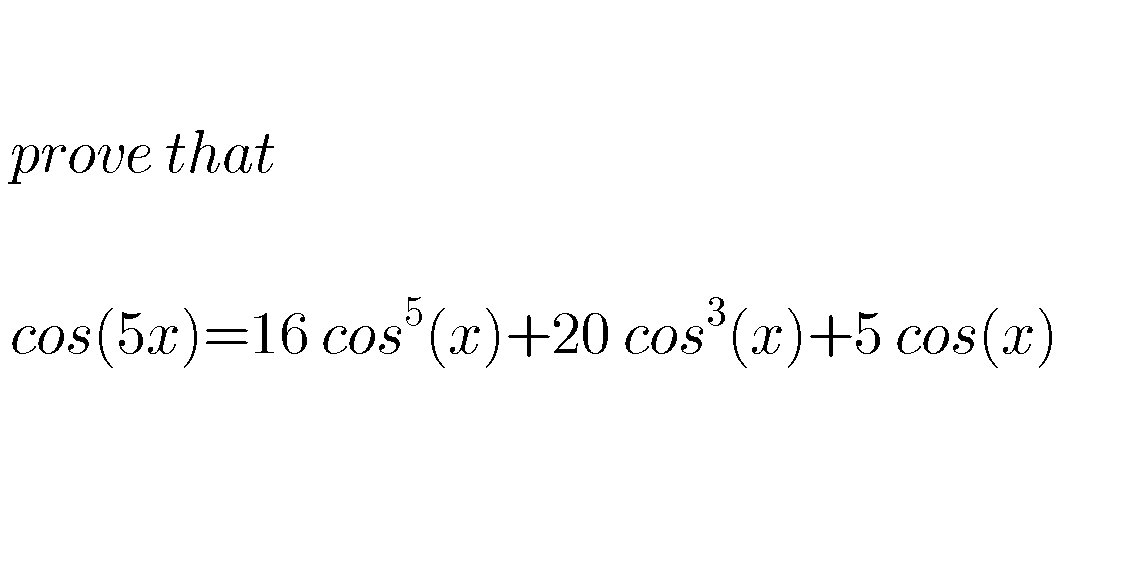
Commented by Prithwish sen last updated on 09/Aug/19
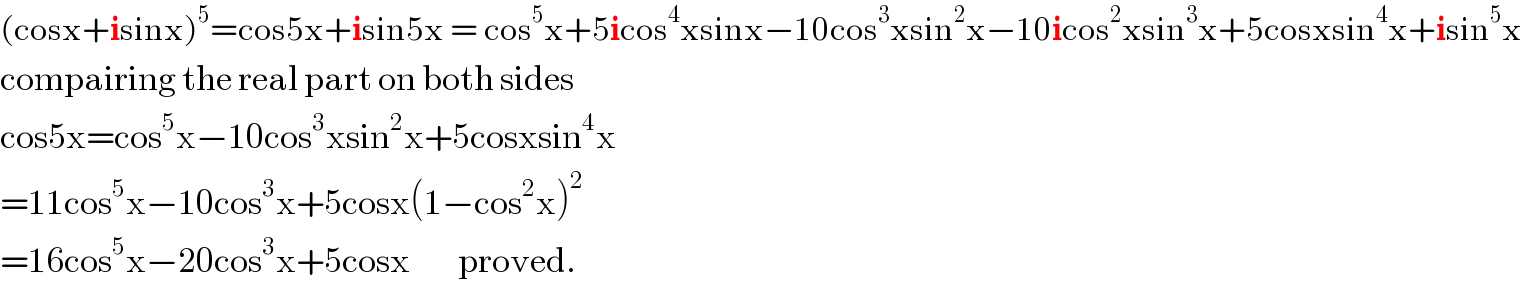
$$\left(\mathrm{cosx}+\boldsymbol{\mathrm{i}}\mathrm{sinx}\right)^{\mathrm{5}} =\mathrm{cos5x}+\boldsymbol{\mathrm{i}}\mathrm{sin5x}\:=\:\mathrm{cos}^{\mathrm{5}} \mathrm{x}+\mathrm{5}\boldsymbol{\mathrm{i}}\mathrm{cos}^{\mathrm{4}} \mathrm{xsinx}−\mathrm{10cos}^{\mathrm{3}} \mathrm{xsin}^{\mathrm{2}} \mathrm{x}−\mathrm{10}\boldsymbol{\mathrm{i}}\mathrm{cos}^{\mathrm{2}} \mathrm{xsin}^{\mathrm{3}} \mathrm{x}+\mathrm{5cosxsin}^{\mathrm{4}} \mathrm{x}+\boldsymbol{\mathrm{i}}\mathrm{sin}^{\mathrm{5}} \mathrm{x} \\ $$$$\mathrm{compairing}\:\mathrm{the}\:\mathrm{real}\:\mathrm{part}\:\mathrm{on}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\mathrm{cos5x}=\mathrm{cos}^{\mathrm{5}} \mathrm{x}−\mathrm{10cos}^{\mathrm{3}} \mathrm{xsin}^{\mathrm{2}} \mathrm{x}+\mathrm{5cosxsin}^{\mathrm{4}} \mathrm{x} \\ $$$$=\mathrm{11cos}^{\mathrm{5}} \mathrm{x}−\mathrm{10cos}^{\mathrm{3}} \mathrm{x}+\mathrm{5cosx}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} \\ $$$$=\mathrm{16cos}^{\mathrm{5}} \mathrm{x}−\mathrm{20cos}^{\mathrm{3}} \mathrm{x}+\mathrm{5cosx}\:\:\:\:\:\:\:\:\mathrm{proved}. \\ $$
