Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 65930 by gunawan last updated on 06/Aug/19

If t=((x^2 −3)/(3x+7)) then log(1−∣t∣) can to find for a. 2<x<6 b.− 2<x<5 c.− 2≤x≤6 d. x≤−2 or x>6 e. x<−1 or x>3

$$\mathrm{If}\:{t}=\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{3}{x}+\mathrm{7}}\:\mathrm{then} \\ $$ $$\mathrm{log}\left(\mathrm{1}−\mid{t}\mid\right)\:\mathrm{can}\:\mathrm{to}\:\mathrm{find}\:\mathrm{for} \\ $$ $$\mathrm{a}.\:\mathrm{2}<{x}<\mathrm{6} \\ $$ $${b}.−\:\mathrm{2}<{x}<\mathrm{5} \\ $$ $${c}.−\:\mathrm{2}\leqslant{x}\leqslant\mathrm{6} \\ $$ $$\mathrm{d}.\:{x}\leqslant−\mathrm{2}\:\mathrm{or}\:{x}>\mathrm{6} \\ $$ $${e}.\:{x}<−\mathrm{1}\:{or}\:{x}>\mathrm{3} \\ $$

Answered by MJS last updated on 06/Aug/19

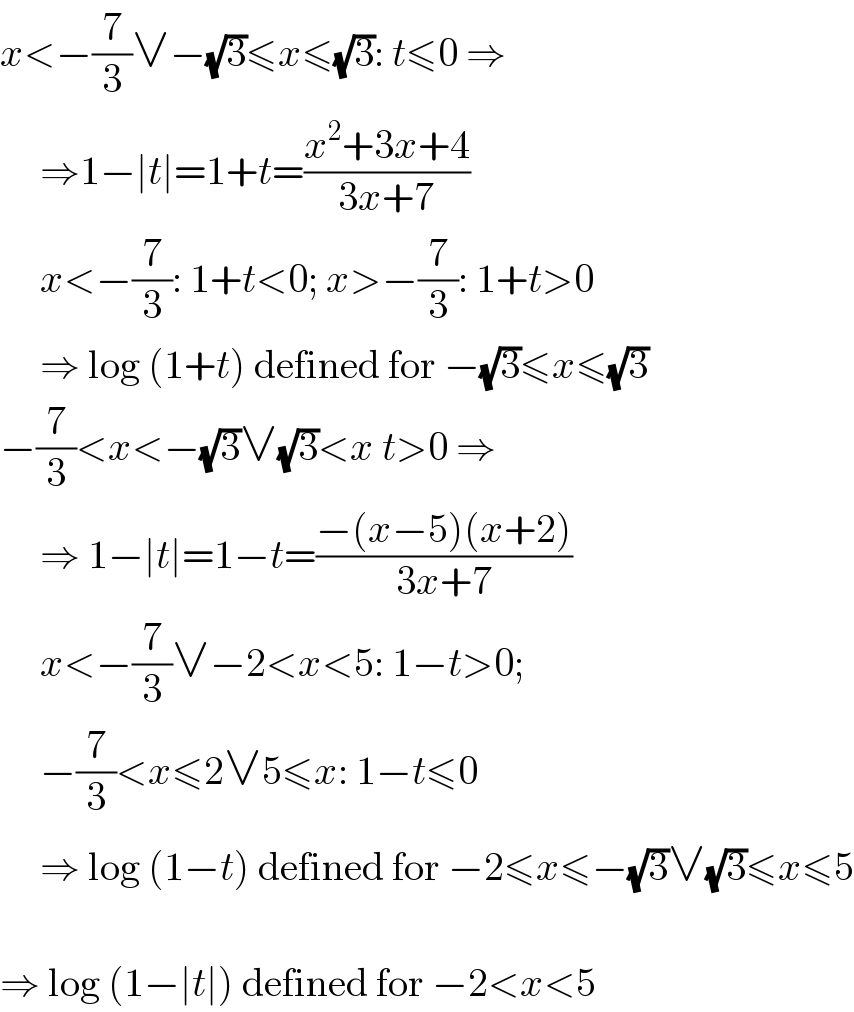
x<−(7/3)∨−(√3)≤x≤(√3): t≤0 ⇒ ⇒1−∣t∣=1+t=((x^2 +3x+4)/(3x+7)) x<−(7/3): 1+t<0; x>−(7/3): 1+t>0 ⇒ log (1+t) defined for −(√3)≤x≤(√3) −(7/3)<x<−(√3)∨(√3)<x t>0 ⇒ ⇒ 1−∣t∣=1−t=((−(x−5)(x+2))/(3x+7)) x<−(7/3)∨−2<x<5: 1−t>0; −(7/3)<x≤2∨5≤x: 1−t≤0 ⇒ log (1−t) defined for −2≤x≤−(√3)∨(√3)≤x≤5 ⇒ log (1−∣t∣) defined for −2<x<5

$${x}<−\frac{\mathrm{7}}{\mathrm{3}}\vee−\sqrt{\mathrm{3}}\leqslant{x}\leqslant\sqrt{\mathrm{3}}:\:{t}\leqslant\mathrm{0}\:\Rightarrow \\ $$ $$\:\:\:\:\:\Rightarrow\mathrm{1}−\mid{t}\mid=\mathrm{1}+{t}=\frac{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{4}}{\mathrm{3}{x}+\mathrm{7}} \\ $$ $$\:\:\:\:\:{x}<−\frac{\mathrm{7}}{\mathrm{3}}:\:\mathrm{1}+{t}<\mathrm{0};\:{x}>−\frac{\mathrm{7}}{\mathrm{3}}:\:\mathrm{1}+{t}>\mathrm{0} \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{log}\:\left(\mathrm{1}+{t}\right)\:\mathrm{defined}\:\mathrm{for}\:−\sqrt{\mathrm{3}}\leqslant{x}\leqslant\sqrt{\mathrm{3}} \\ $$ $$−\frac{\mathrm{7}}{\mathrm{3}}<{x}<−\sqrt{\mathrm{3}}\vee\sqrt{\mathrm{3}}<{x}\:{t}>\mathrm{0}\:\Rightarrow \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{1}−\mid{t}\mid=\mathrm{1}−{t}=\frac{−\left({x}−\mathrm{5}\right)\left({x}+\mathrm{2}\right)}{\mathrm{3}{x}+\mathrm{7}} \\ $$ $$\:\:\:\:\:{x}<−\frac{\mathrm{7}}{\mathrm{3}}\vee−\mathrm{2}<{x}<\mathrm{5}:\:\mathrm{1}−{t}>\mathrm{0}; \\ $$ $$\:\:\:\:\:−\frac{\mathrm{7}}{\mathrm{3}}<{x}\leqslant\mathrm{2}\vee\mathrm{5}\leqslant{x}:\:\mathrm{1}−{t}\leqslant\mathrm{0} \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{log}\:\left(\mathrm{1}−{t}\right)\:\mathrm{defined}\:\mathrm{for}\:−\mathrm{2}\leqslant{x}\leqslant−\sqrt{\mathrm{3}}\vee\sqrt{\mathrm{3}}\leqslant{x}\leqslant\mathrm{5} \\ $$ $$ \\ $$ $$\Rightarrow\:\mathrm{log}\:\left(\mathrm{1}−\mid{t}\mid\right)\:\mathrm{defined}\:\mathrm{for}\:−\mathrm{2}<{x}<\mathrm{5} \\ $$

Commented bygunawan last updated on 06/Aug/19

thank you Sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com