
Question Number 65841 by Rio Michael last updated on 04/Aug/19
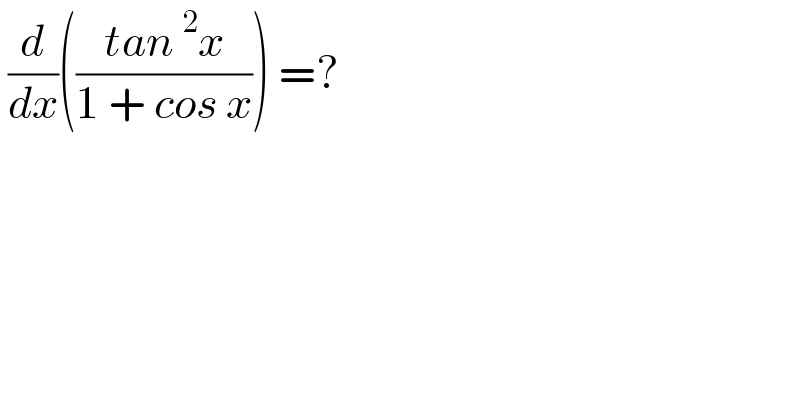
$$\:\frac{{d}}{{dx}}\left(\frac{{tan}\:^{\mathrm{2}} {x}}{\mathrm{1}\:+\:{cos}\:{x}}\right)\:=? \\ $$
Commented by som(math1967) last updated on 05/Aug/19
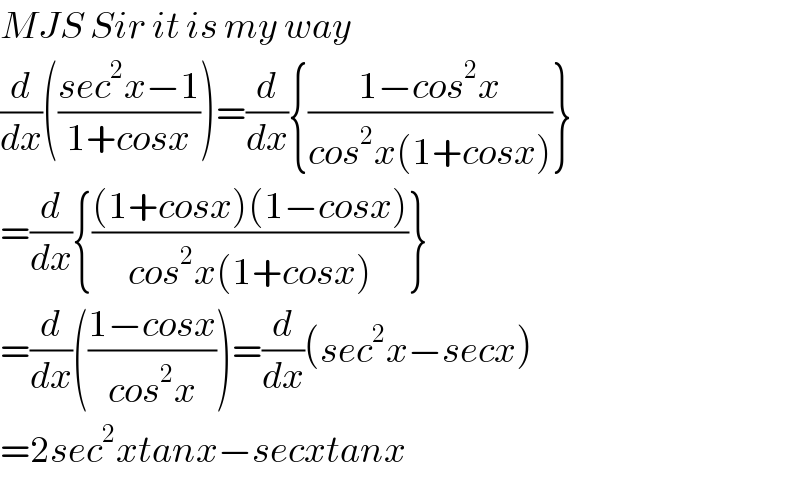
$${MJS}\:{Sir}\:{it}\:{is}\:{my}\:{way} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{sec}^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{1}+{cosx}}\right)=\frac{{d}}{{dx}}\left\{\frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} {x}\left(\mathrm{1}+{cosx}\right)}\right\} \\ $$$$=\frac{{d}}{{dx}}\left\{\frac{\left(\mathrm{1}+{cosx}\right)\left(\mathrm{1}−{cosx}\right)}{{cos}^{\mathrm{2}} {x}\left(\mathrm{1}+{cosx}\right)}\right\} \\ $$$$=\frac{{d}}{{dx}}\left(\frac{\mathrm{1}−{cosx}}{{cos}^{\mathrm{2}} {x}}\right)=\frac{{d}}{{dx}}\left({sec}^{\mathrm{2}} {x}−{secx}\right) \\ $$$$=\mathrm{2}{sec}^{\mathrm{2}} {xtanx}−{secxtanx} \\ $$
Answered by MJS last updated on 04/Aug/19
![(d/dx)[(u/v)]=((u′v−uv′)/v^2 )= u=tan^2 x → u′=2((tan x)/(cos^2 x))=2((sin x)/(cos^3 x)) v=1+cos x → v′=−sin x =((2((sin x)/(cos^3 x))(1+cos x)+tan^2 x sin x)/((1+cos x)^2 ))= ... =(((2−cos x)tan x)/(cos^2 x))](Q65844.png)
$$\frac{{d}}{{dx}}\left[\frac{{u}}{{v}}\right]=\frac{{u}'{v}−{uv}'}{{v}^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:{u}=\mathrm{tan}^{\mathrm{2}} \:{x}\:\rightarrow\:{u}'=\mathrm{2}\frac{\mathrm{tan}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{2}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}^{\mathrm{3}} \:{x}} \\ $$$$\:\:\:\:\:{v}=\mathrm{1}+\mathrm{cos}\:{x}\:\rightarrow\:{v}'=−\mathrm{sin}\:{x} \\ $$$$=\frac{\mathrm{2}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}^{\mathrm{3}} \:{x}}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)+\mathrm{tan}^{\mathrm{2}} \:{x}\:\mathrm{sin}\:{x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }= \\ $$$$... \\ $$$$=\frac{\left(\mathrm{2}−\mathrm{cos}\:{x}\right)\mathrm{tan}\:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$
