
Question Number 657 by 123456 last updated on 21/Feb/15
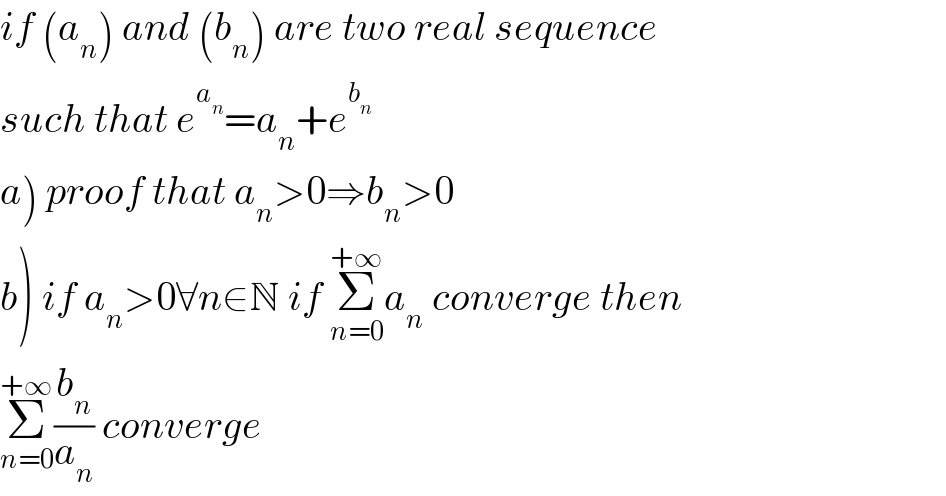
$${if}\:\left({a}_{{n}} \right)\:{and}\:\left({b}_{{n}} \right)\:{are}\:{two}\:{real}\:{sequence} \\ $$ $${such}\:{that}\:{e}^{{a}_{{n}} } ={a}_{{n}} +{e}^{{b}_{{n}} } \\ $$ $$\left.{a}\right)\:{proof}\:{that}\:{a}_{{n}} >\mathrm{0}\Rightarrow{b}_{{n}} >\mathrm{0} \\ $$ $$\left.{b}\right)\:{if}\:{a}_{{n}} >\mathrm{0}\forall{n}\in\mathbb{N}\:{if}\:\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{a}_{{n}} \:{converge}\:{then} \\ $$ $$\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{{b}_{{n}} }{{a}_{{n}} }\:{converge} \\ $$
Answered by prakash jain last updated on 20/Feb/15
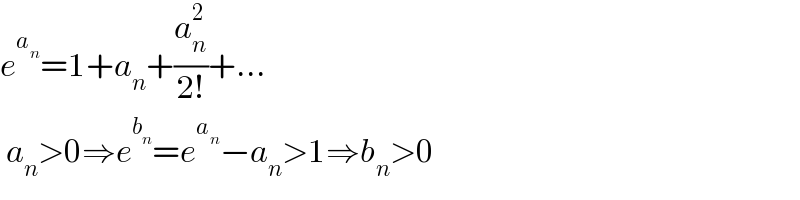
$${e}^{{a}_{{n}} } =\mathrm{1}+{a}_{{n}} +\frac{{a}_{{n}} ^{\mathrm{2}} }{\mathrm{2}!}+... \\ $$ $$\:{a}_{{n}} >\mathrm{0}\Rightarrow{e}^{{b}_{{n}} } ={e}^{{a}_{{n}} } −{a}_{{n}} >\mathrm{1}\Rightarrow{b}_{{n}} >\mathrm{0} \\ $$
